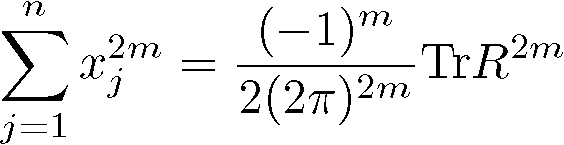春休みのちょっと時間のあるときに更新してしまおうと思ったのですが、アノマリーインフローを説明するのに３回にもなってしまいました . . . 。もっと簡単にできると思ったのですが、こういうサイト記事にすると結局いろいろ説明が必要でした。しかも「最近の研究から」とかいうカテゴリーなのに全然最近の研究の話じゃなくて、何やってるんだろう、という感じですが、ここまできたので話をまとめてしまいたいと思います。

前回までで、M5 ブレインのアノマリーの「アノマリー多項式」は、前回の記号で +  だ、ということをお話ししました。これを、前回のようにチャーンクラスで表すと

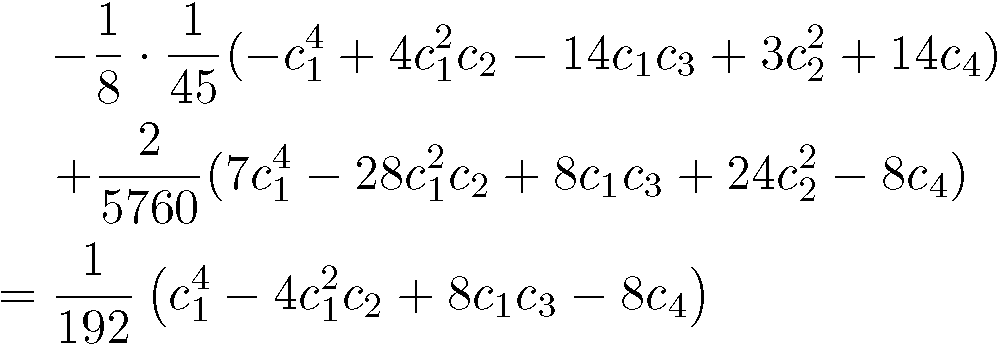
となり、さらにこれを前回書いたように 実ベクター束の曲率形式で表すと

となります。これを  と書くことにします。この8次微分形式がM5 ブレインのアノマリーのアノマリー多項式です。

このアノマリー多項式から M5 ブレインのアノマリーは次のようにして得られます。まず、アノマリー多項式の常として  は完全、つまり d(なんとか) と書けます。これをと書いたとしましょう。この  をゲージ変換、つまり今の場合はローカルローレンツ変換  したとすると、その変化分  はまた完全になります。すなわちと書けます。この  の ー 倍がアノマリー、つまり量子論的な有効作用をゲージ変換したときの変化分になります。

注　この時点では  の + 倍なのか、ー 倍なのかよくわかりません。実際 Duff-Liu-Minasian のオリジナル論文では、この+ 倍をキャンセルするように補正項をいれています。また、Becker-Becker オリジナル論文でもそうなっています。ところが後の Becker-Becker-Schwarz の教科書では補正項の符号が逆になっており（(10.46)式）、それが現代のコンセンサスになっているようです。なお、 M理論でなくタイプIIA 理論において、Vafa-Witten によってDuff-Liu-Minasian より早くこのような補正項の存在が指摘されています。その結果はディラトンによらないので、タイプIIA 理論の強結合極限であるM理論にも対応する項が存在することが帰結されますが、その結果からはどちらの符号が正しいかは簡単にはわかりません（ユークリッド化されているので虚数 i が現れている）。しかし、その後の Sethi-Vafa-Witten では、 となっているのでBecker-Becker-Schwarz の教科書と同じ符号になります。また、Denef のレビューでは、補正項の符号は Becker-Becker-Schwarz の教科書と逆（Duff-Liu-MinasianやBecker-Becker オリジナル論文と同じ）ですが、  の積分が（後で見るように）オイラー数のー24分の1になるべきところ、＋24分の1と思いっきり書いてあるので結果的に Becker-Becker-Schwarz の教科書の結論と同じになります。ここまで注でした

さて、こうしてやっと M5 ブレインのアノマリーの具体形を書くことができました！この   は M5 の世界体積が曲がっていれば０ではありません。ということは、アノマリー（の ー 分の１）  も０でない、ということなので、これはゲージアノマリーの一種なので、これはまずい、ということになります。ローカルローレンツアノマリーは一般座標変換のアノマリーとカウンタータームを付け加えることによって移り合いますから、このもとで理論が不変になっていない、ということは、エネルギー運動量が保存しない、ということを意味するからです。これをどうしたらいいでしょうか？

これを解決するのがアノマリーインフロー機構です。要するに、エネルギー運動量はブレインの外から流れ込んできているんだ！と考えるのです。

M5 ブレインは11次元時空に埋め込まれています。なので、 M5 ブレインだけを取り出して何らかの保存則を考えるのではなく、11次元全体で見れば保存していればいい、とする考え方です。この機構が実際に実現していることは、次のように数式で見ることができます。

まず、M理論の（ボゾニック）アクションを

とします。 はいつもの11次元超重力アクション、 は M2と M5 のブレインアクションです。（ の前の符号は、普通の4次元電磁気学で（＋ーーー）符号のときの荷電粒子の作用と同じ符号ですが、電磁気で（ー＋＋＋）符号の時にそうすると、Maxwell 方程式が divE=ーρ などとなることになります。しかし、別に間違いではないのでいろいろな文献と同じにしておきます。 の前の符号の方は、正しくアノマリーインフローが起きるような符号になるように  が定義されているとします。）それらに加えて、ここでは という新たな項を入れました。この項があると何が起こるのでしょうか？

そのためには、これをゲージ（ローカルローレンツ）変換してみるとわかります。まず、 なので、部分積分すると、

となります。d が 3-form を飛び越えるので、部分積分しても符号が変わらないことに注意してください。これをゲージ変換すると、 ですからこれも部分積分すると、今度は飛び越えるのが偶数-form なので今度は符号が出て、

となります。すると、M5-ブレインがあるとそれは のソースなので   を代入するとM5-ブレイン上の6次元積分になって、

となります。ここで、最後の行ではディラック・シュビンガー・ツバンツィガーのチャージ量子化条件を使いました。これはアノマリーのマイナスです！（上の　注　参照）したがって、このアノマリーインフロー項があると、 M5-ブレインのような のソースにはアノマリーが「流れ込ん」で、ちょうどアノマリーをキャンセルするのです！

ここまででやっと Duff-Liu-Minasian の紹介が終わりました。さて、ここから先、この項の存在の必要性がわかって、それが何を意味することがわかったのか、それがポルチンスキーに書いてない超重大事実だと言いたいのですが、それはやっぱりもう１回使って次の記事に書くことにしましょう。

前回のおわりにも書いたように、アノマリー多項式という言葉自体はポルチンスキーにも出てきますが、M5 の話ではないのでその場合について具体的に書きたいと思います。

アノマリー多項式というのは、考えている理論の時空の次元より２高い次数の微分形式で、それに「降下方程式（descent equation）」と呼ばれる簡単な代数演算を行うと望みの理論のアノマリーが得られる、という大変便利な式です。アノマリー多項式は一般に何らかの（そのアノマリーを出すカイラルな場が結合している）場の曲率２次形式のなんとか乗のトレースの多項式になっているので、もっとちゃんと言うと、考えているベクター束の「チャーンルート」、つまり曲率の固有値の対称多項式で表されているので、そう呼ばれています。

ここのところはグリーン・シュワルツ・ウィッテンの教科書第２巻にすでにでていて、こうこれはいくら古くても朽ちることのない事実です。それによれば、M5 ブレイン上の場のうちアノマリーを出す２つの種類の場である、セルフデュアル2-フォーム場 とカイラルなシンプレクティックマヨラナスピナー のよる重力アノマリーは、それぞれ「ヒルツェブルフL-多項式(Hilzebruch L-polynomial)」と「A- ルーフジーナス(A-roof genus)」

から読み取れます。ここで、 はチャーンルートと言って、複素ベクターバンドルの曲率形式  の j 番目の固有値  と
のように関係しています。複素 n 次元なら  は U(n) リー代数に値をもつ 2-form なので、  は実数（に値をもつ 2-form）です。

もっとも、細かいことを言うと、今アノマリーを考えているのは M5-ブレインの世界体積(“world volume”)なので、その空間の符号は Lorentzian 、すなわち「時空」です。アノマリーを一番最初に習うときにでてくる三角アノマリーも４次元「時空」で考えています。なので、そこに出てくる曲率形式は（特に今の場合は重力アノマリーを考えているので）SO(2n-1,1) に値をとるので、複素ベクター束の標準接続の曲率形式や、これからやるようにそれをSO(2n)実ベクトル束と見たりするのはおかしいようにも思えます。しかし、そこのところは藤川メソッドをやるときのように「ユークリッド化」をしていると考えて、それで結局すべてうまくいくことがわかります。なので、ここではそういうツッコミはしないことにして先に進みましょう。このようにして出てくるアノマリー多項式からアノマリーインフローを引き起こす補正項の存在が帰結され、それが超弦のコンパクト化に重大な拘束条件をもたらす、というところまで話してやっと「ポルチンスキーの教科書が書かれた後になってわかった. . .」になるのですが、そのときには曲率形式は（カラビ・ヤウだったりする）コンパクトな方向だけ値をもつものを考えます。

話を元に戻して、上の  や  を展開すると、各項は  の対称式にまとまり、チャーンクラス

を使って

となります。これらのチャーンクラス  は基本対称式なので  の積の和で書くことができます。さらに、複素ベクター束の曲率形式  が

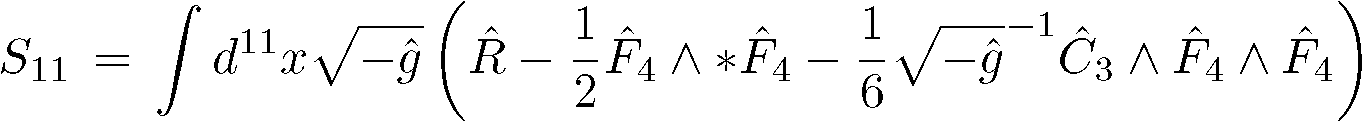
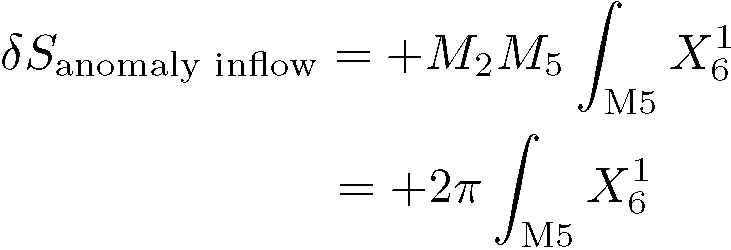
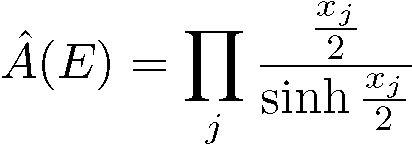
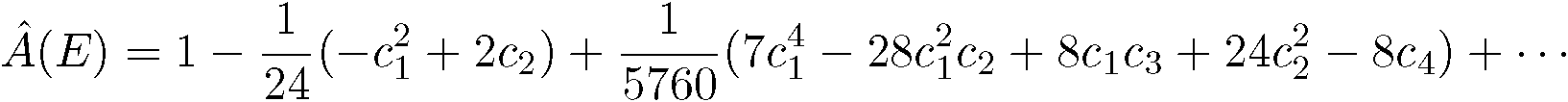
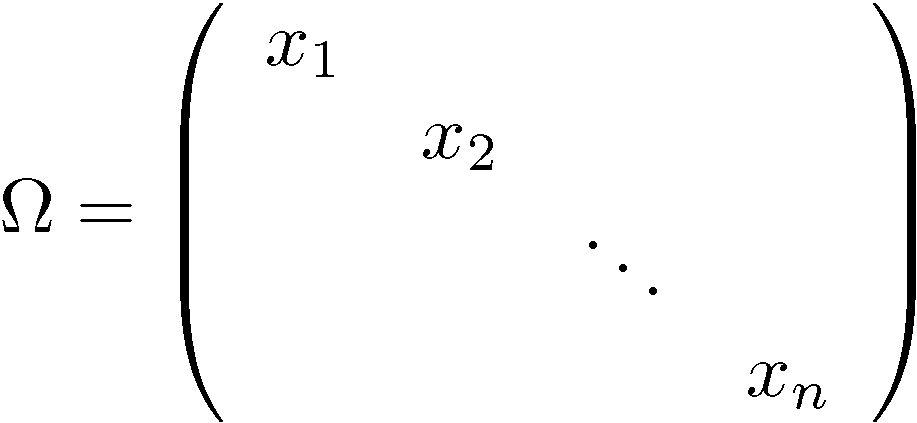のとき、この複素ベクター束を実ベクター束と見たときの曲率形式  はなので

と書けます。

さて、これでやっと M5 のアノマリー多項式がどう言うものなのかを記述することができます。知られていることは、６次元のセルフデュアル2-フォーム場  のアノマリーのアノマリー多項式は  の  4次の項、シンプレクティックマヨラナスピナー のアノマリーのアノマリー多項式は の  4次の項で与えられる、ということです。これらは8次の微分形式なのでそれぞれ  ,   と書くことにすると、これらを足したものが M5 のアノマリー多項式です。

ここまでこの回もかなり長くなってしまったので、このアノマリー多項式が実際のアノマリーとどういう関係になっていて、そのようにして表されたアノマリーはあってもいいのか、それがどのように考えられたのかについては次の回に書くことにしましょう。