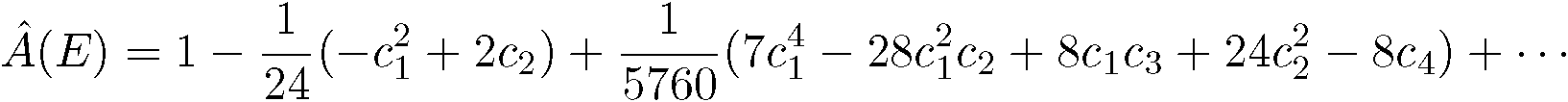前回のおわりにも書いたように、アノマリー多項式という言葉自体はポルチンスキーにも出てきますが、M5 の話ではないのでその場合について具体的に書きたいと思います。

アノマリー多項式というのは、考えている理論の時空の次元より２高い次数の微分形式で、それに「降下方程式（descent equation）」と呼ばれる簡単な代数演算を行うと望みの理論のアノマリーが得られる、という大変便利な式です。アノマリー多項式は一般に何らかの（そのアノマリーを出すカイラルな場が結合している）場の曲率２次形式のなんとか乗のトレースの多項式になっているので、もっとちゃんと言うと、考えているベクター束の「チャーンルート」、つまり曲率の固有値の対称多項式で表されているので、そう呼ばれています。

ここのところはグリーン・シュワルツ・ウィッテンの教科書第２巻にすでにでていて、こうこれはいくら古くても朽ちることのない事実です。それによれば、M5 ブレイン上の場のうちアノマリーを出す２つの種類の場である、セルフデュアル2-フォーム場 とカイラルなシンプレクティックマヨラナスピナー のよる重力アノマリーは、それぞれ「ヒルツェブルフL-多項式(Hilzebruch L-polynomial)」と「A- ルーフジーナス(A-roof genus)」

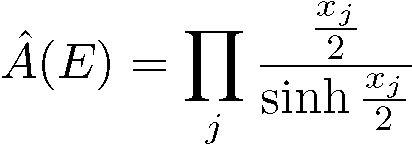から読み取れます。ここで、 はチャーンルートと言って、複素ベクターバンドルの曲率形式  の j 番目の固有値  と
のように関係しています。複素 n 次元なら  は U(n) リー代数に値をもつ 2-form なので、  は実数（に値をもつ 2-form）です。

もっとも、細かいことを言うと、今アノマリーを考えているのは M5-ブレインの世界体積(“world volume”)なので、その空間の符号は Lorentzian 、すなわち「時空」です。アノマリーを一番最初に習うときにでてくる三角アノマリーも４次元「時空」で考えています。なので、そこに出てくる曲率形式は（特に今の場合は重力アノマリーを考えているので）SO(2n-1,1) に値をとるので、複素ベクター束の標準接続の曲率形式や、これからやるようにそれをSO(2n)実ベクトル束と見たりするのはおかしいようにも思えます。しかし、そこのところは藤川メソッドをやるときのように「ユークリッド化」をしていると考えて、それで結局すべてうまくいくことがわかります。なので、ここではそういうツッコミはしないことにして先に進みましょう。このようにして出てくるアノマリー多項式からアノマリーインフローを引き起こす補正項の存在が帰結され、それが超弦のコンパクト化に重大な拘束条件をもたらす、というところまで話してやっと「ポルチンスキーの教科書が書かれた後になってわかった. . .」になるのですが、そのときには曲率形式は（カラビ・ヤウだったりする）コンパクトな方向だけ値をもつものを考えます。

話を元に戻して、上の  や  を展開すると、各項は  の対称式にまとまり、チャーンクラス

を使って

となります。これらのチャーンクラス  は基本対称式なので  の積の和で書くことができます。さらに、複素ベクター束の曲率形式  が

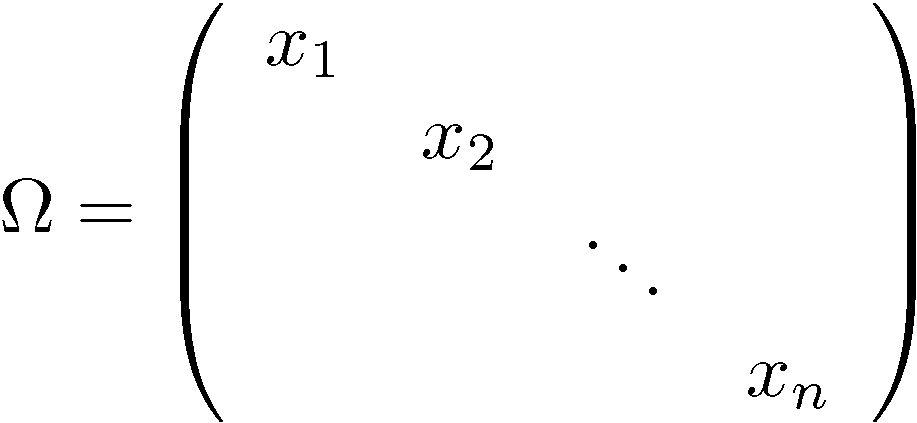のとき、この複素ベクター束を実ベクター束と見たときの曲率形式  はなので

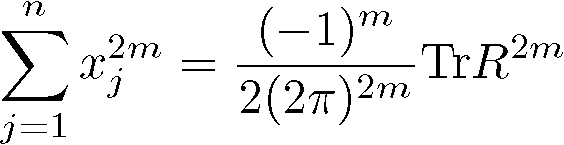
と書けます。

さて、これでやっと M5 のアノマリー多項式がどう言うものなのかを記述することができます。知られていることは、６次元のセルフデュアル2-フォーム場  のアノマリーのアノマリー多項式は  の  4次の項、シンプレクティックマヨラナスピナー のアノマリーのアノマリー多項式は の  4次の項で与えられる、ということです。これらは8次の微分形式なのでそれぞれ  ,   と書くことにすると、これらを足したものが M5 のアノマリー多項式です。

ここまでこの回もかなり長くなってしまったので、このアノマリー多項式が実際のアノマリーとどういう関係になっていて、そのようにして表されたアノマリーはあってもいいのか、それがどのように考えられたのかについては次の回に書くことにしましょう。