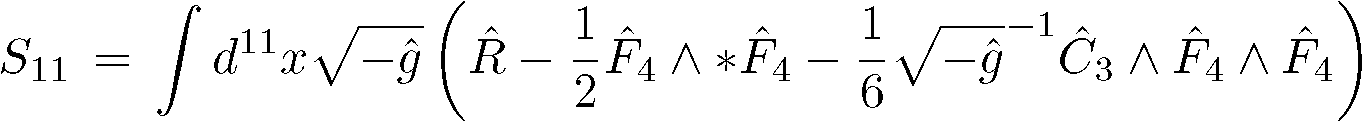これまで３回にわたってアノマリーインフローについて説明してきました。その３の注でも書きましたが、ここまで全然「ポルチンスキーの教科書が書かれた後」ではありません。また、これからこの回で書くこともポルチンスキーの教科書が出版される前にわかっていたことです。しかし、その事実がその後注目され、現代の超弦理論では常識になっているのに書かれていない重要事実として、多くに人に知ってもらうためにこの記事を書いています。なぜなら「超弦を勉強するのに何がいいですか？Zweibach? Polchinski?」などと聞かれることがよくあるからです。そんなんじゃ全然たりないんですー！と言いたいのです。（ちなみに、Becker-Becker-Schwarz の教科書には（自分たちが（下のことを）見つけただけあって）第10章に出ています。なお、ここでは  と置いています。）

さて本題に戻って、前回、M5-ブレインのアノマリーが相殺されるためには、M理論の低エネルギー作用には11次元超重力にはなかった

という項が必要なんだ、ということを書きました。この項は、X8 が時空の曲率の４次式ですから、微分を8個も含む高次微分項です。なので、微分を2個までしか含まない条件で作られた超重力には当然現れません。したがって、低エネルギーではローカルにはほとんど効かなくなりますが（微分が多いほど低エネルギーでサプレスされる）、グローバルには無視できない寄与をします。

この状況は、ヘテロティック弦のグリーン・シュワルツ項とよく似ています。これも、10次元超重力にはないが、ヘテロティック弦の（素朴には存在する）アノマリーがグリーン・シュワルツ機構で相殺されるために必要な項です。これも高次微分項でした。そして、グリーン・シュワルツ機構において B場がゲージ変換してしまうために、場の強さ H のビアンキ恒等式が dH=0 でなく

に変更されたのでした。そしてさらに、このことから「（dH=0 なら）TrR^2 が0でないならば、TrF^2 も0にはできない」ということがわかります。もっとちゃんというと、左辺はコホモロジーとして０なので、それらは同じコホモロジークラスに属さなければならない、ということを意味します。つまり、「数式は言葉です。計算じゃない。」とおっしゃった受験物理のカリスマ、苑田さん流に言うと、「内部空間が曲がっていたら、内部ゲージ場も曲がっていなければならない」ということになります。この事実によって、ヘテロティック弦においてカラビ・ヤウのスピンコネクションをゲージコネクションに埋め込む standard embedding という考え方が初期のヘテロティック理論で考えられました。その一方で、SU(3) でない曲がり（カラビ・ヤウ 3-fold は SU(3)ホロノミー）をゲージバンドルでどう実現すればいいかは（これもポルチンスキーの教科書が出版されるのと前後して発表された）Friedman-Morgan-Witten の結果を待たなければなりませんでした。

それでは、今の  はどんな働きをするのでしょうか。それを見るために、前回のM理論のアクション

から  の運動方程式を求めてみましょう。Form を使った式で書くと、結果は

となります。

この式が欲しくて３回も記事を書いてきました。この式は  の運動方程式、あるいはその双対  のビアンキ恒等式です。それが、ヘテロティックのときと同じように変更を受けている、と見ることができます。これは8次の微分形式ですが、ここで M理論をある境界のない8次元コンパクト空間 Z で3次元にコンパクト化するとして、その8次微分形式を Z で積分してみましょう。すると、最初の項は０になります。次の項は単にフラックスの積分  です。その次の項は、M2ブレインが  枚 Z に含まれていれば  になります。さて最後に、 の積分は、計算してみると（カラビ・ヤウ、c1＝0 の場合） Z のオイラー数のマイナス２４分の１：

になることが示せます。よって結局

となります！これが示したかった式でした。

これはタドポール条件と呼ばれています。なにかのファインマン図形のような図形を書いたとき、１本の外線から書きはじめて、それ以外に別の外線がなくてループで終わるような物を書くとオタマジャクシのような形になります。それと同じように、内部空間にフラックスがどこかから湧き出したら、それがどこにも吸い込まれて行くところがないと困るので、タドポールがないようにせよ、と言うのです。この場合、時空の曲がり（オイラー数）がフラックスの吸い込みの役割を果たすことがわかります。この事実は、のちのフラックスコンパクト化を用いた超弦による初期宇宙論において、考慮されるべき重要な条件となったのです。

以上で「ポルチンスキーの教科書が書かれた後」、ではないのですが、ポルチンスキーには書いてなくて、「後になって『その重要性が』わかった」ことの一つを書くことができました！この事実は、11次元を3次元にコンパクト化するときの条件なので、4次元物理や素粒子の標準模型の実現とは全く関係のないことのように見えるかもしれません。ところが実はーこれもポルチンスキーに書いてないことですがーこの8次元多様体として楕円ファイブレーションを許す、つまり何かの6次元多様体上の各点各点に2次元トーラスが「生え」ているようなものの全体空間で表されるようなものを考えると、そのトーラスの体積→0 の極限で理論は3次元から4次元となり、しかもそのトーラスがつぶれたところから大統一理論に出てくるようなE型系列のゲージ対称性が実現するのです！これが「F理論」です。したがって、この制限は、現代の超弦による素粒子模型構築において、大変重要な意味をもっています。この F理論 についてもいつか記事を書かないといけないですね。次回はいつになるかわかりませんが . . . 。