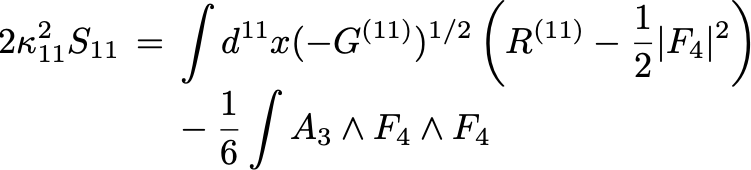「その１（の予定）」と書いてから、やらなければならないことが怒涛のようにやってきて、オリピックが２回も終わってしまいました. . . 。やっと少し余裕がでてきたので、遅ればせながらその２を書いてみたいと思います。

ポルチンスキーが書かれた後になってわかった、ポルチンスキーに書いてない超弦理論の重要事実として、何よりもまず最初にあげなければならないことは、M理論における重力チャーン・サイモンズ(gravitational Chern-Simons)項の存在でしょう。

「M理論」というのは、「11次元超重力理論を低エネルギー有効作用としてもつような、弦理論ではないが何らかの広がったオブジェクトを基本的構成要素としてもつ理論」のことです。広がったオブジェクトに関してはもう少し詳しくわかっていて、11次元超重力が「足」（添字）３つをもつ３階テンソル場を含むことから、M理論は２次元的に広がった「膜」＝「メンブレイン(membrane)」の理論である、と考えられています。授業では、タイプIIA弦の強結合極限である、と教えます。このことはポルチンスキーにも書いてあります。

超昔の Green-Schwarz-Witten の教科書を読むと、11次元超重力は超弦理論の低エネルギー理論ではない（もしそうなら10次元のはずだから）のに存在するので “enigma” だ、などと書いてあります。それから10年がたって、Witten が1995年に、タイプIIA弦の強結合極限として現れる11次元理論の存在を指摘したのでした。

メンブレインは量子化が難しく、超弦のように世界面理論（この場合は１次元の物体が掃く２次元面でなく、２次元が掃く３次元「世界体積理論」）から構成的に定義できないので、行列模型(「行列理論（”Matrix theory”）」と呼ばれる )やある種の３次元チャーン・サイモンズ理論を用いた理論(ABJM theory)など、さまざまな定式化が提唱されてきました。しかし、超弦宇宙論のようにM理論の幾何学的情報を使ってさまざまな議論をするときには、やはり11次元超重力を基に考えることになります。

超重力理論というと一般には非常に面倒な計算を伴うものですが、11次元超重力のように超対称性が非常に高いものは比較的簡単でシンプルな理論です。実際、フェルミオン場を落としてボゾン場だけにすると、11次元超重力の作用は次のような簡単なものになります：

ここで、微分形式はいつものように

などで、またポルチンスキーの教科書の記法

を使っています。

11次元超重力だとたったこれだけなのですが、M理論がタイプIIA弦の超結合極限の理論なら、もちろんこれだけで終わるはずはありません。質量を持たない場に限ったとしても、微分を２つより多く含むような項も無限に存在する可能性がありますが、それらは低エネルギーでは落としている、という立場を取っています。そのような高次微分項として、どんなものが含まれるかを決めることは簡単ではありません。しかし例外的に、11次元超重力に存在する「M5-ブレイン」とよばれるブレイン上の理論のアノマリー（anomaly）（＝「量子異常」）が相殺されるために必要である、というロジックで、ある特別な項の存在を議論することができます。これが　Duff, Liu, Minasian らによって1998 年に明らかにされた、「アノマリーインフロー(anomaly inflow)」を引き起こす「重力チャーン・サイモンズ項」です。注

次回、（いつになるかわかりませんが. . . ）このことについてもっと詳しく説明したいと思います。この項が存在することによって、超弦理論におけるワープしたコンパクト化に対する（それまであった） no-go 定理が回避できたのです。

注  Vafa と Witten によっても別の議論によってこの項の存在が指摘されました。