NSEの基礎
1.1 中性子散乱とは
1.2 中性子非弾性散乱
2.1 中性子スピンエコーの特徴
2.2 中性子スピンエコーの原理
3.1 NSEの装置
3.2 世界のNSE分光器
4.1 NSEデータの意味
4.2 NSEデータの解析
第2章に書いたように、NSEの装置は第一歳差磁場と第二歳差磁場で(実質的に)同じだけ回転して元に戻るように調整してありますので、弾性散乱だけを測定すればすべての中性子スピンがカウンター前の偏極アナライザを通ります。しかし、もし一部の中性子が試料での非弾性散乱によって速度が変わると、その中性子はスピンの回転角にずれが生じます。このずれの角度をφnetと置くと、偏極アナライザを通る中性子スピンは、本来の中性子強度の ((1+cosφnet)/2) 倍になります。
ところで中性子散乱において、ある角度2θに散乱される中性子の強度は動的構造因子S(Q,ω)(ここでQ=4πsinθ/λ)に比例します。従ってNSE装置を通ってきた中性子の強度は
![]() (4.1)
(4.1)
と書くことができます。ここで非弾性散乱が起きたことによる回転角のずれφnetは、
![]() (4.2)
(4.2)
と書けます。ωは中性子が得た(失った)エネルギー、γとmnは中性子の磁気回転比と質量で、λは入射中性子の波長です。またDは「磁場積分」と呼ばれる量で、中性子の飛程をLとして次のように定義されます。
(4.3)
(4.2)式のうちωに関係しない部分は時間の次元を持ちます。これをFouirer timeと呼び、tと置きます。
(4.4)
(4.1)式に入っている積分範囲の下限-Eは入射中性子のエネルギーですが、これはエネルギー遷移よりも遥かに大きいので下限を-∞としても本質的には同じでしょう。更にS(Q,ω)=S(Q,-ω)と考えても良いので、式(4.1)の2項目はFourier 変換だと考えることができます。すなわち、
これは、動的構造因子S(Q,ω)のフーリエ変換で「中間相関関数」と呼ばれるものです。Fourier timeのtは実時間ではありませんが、空間相関S(Q)が時間と共にどのように変化するかを平均として示したものだ、と言って良いでしょう。これを図で書くと次のように考えることができます。
.gif) |
|
|
赤い色で示した散乱体がt=0で空間的に分布していたとして、その空間相関(例えば小角散乱)を取ると右のようになる、と考えます。この散乱体が時間と共に移動している、あるいは変形しているとすると、平均の位置(青で示した部分)との重なりは時間と共に減少していきます。(もちろん、振動していれば周期的に減ったり増えたりします。)この「重なり」の部分の相関が時間と共にどう変化するか、というのがI(Q,t)です。上のI(Q)の図に時間軸tを加えて書くと次のようになります。
|
|
|
|
ブラウン運動のような単純な拡散の場合は、
I(Q,t)=I(Q,0) exp(-DQ2t)
のようになります。すなわち、Qの値によって上の右側のようなグラフが得られます。これをどのようなモデルによって説明するかが、NSEのデータの処理の最終目標と言うことになります。
次に、実際の測定データとその解析について考えてみましょう。知りたいのは、散乱された中性子のうち非弾性散乱成分がどれくらい含まれるかと言うことです。NSEでは、これを「エコー条件」に合う(すべての中性子スピンの回転角が戻るように2つの歳差磁場コイルの磁場積分の値を合わせてある)時のスピン偏極率として測定します。それは、すべての中性子が弾性散乱すればすべてのスピンが揃うためスピン偏極率が1になりますが、非弾性散乱成分が増えれば増えるほどスピン偏極率が下がるからです。これは、ある散乱角2θに中性子カウンターをセットし、歳差磁場コイルの磁場積分をDとして完全弾性散乱(通常はシリカゲルやグラファイトなど、完全弾性散乱体であると思われる標準試料を用いる)のスピン偏極率P'と非弾性散乱成分を含む試料からの散乱のスピン偏極率Pを用いて
S(Q,t)=P/P' (4.5)
により求めることができます。ここでQは中性子の平均波長λと散乱角2θから、tは磁場積分Dと波長λから計算できます。
このスピン偏極率Pを測定するにはエコー条件のみで中性子の強度を測定すれば良さそうですが、実際の実験ではそれはそう簡単ではありません。装置をエコー条件に揃えたつもりでも、その条件は周辺の装置等微妙な環境の変化ですぐにずれてしまいますし、またいろいろな装置定数も考慮に入れる必要があるからです。そこでまず、エコー条件がずれても対応できるように、またバックグラウンドの影響を考慮できるように第一歳差磁場コイルと第二歳差磁場コイルの磁場積分の値を微妙に変化させて測定します。するともし完全に単色化された中性子を用いれば、次のようなプロファイルになるでしょう。
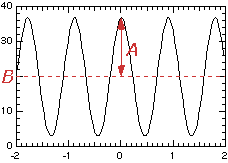 |
|
|
この関数形は
![]() (4.6)
(4.6)
で、iは横軸(第一歳差磁場コイルと第二歳差磁場コイルの電流の差〜これを「シンメトリーコイル」で調節します)の電流値、i0はエコー中心の電流値です。ここで得られるAとBの値、及びflipping ratioと呼ばれる装置定数R(これはフリッパーを働かせた場合の強度Ionと切った場合の強度Ioffを用いてR=(Ion-Ioff)/(Ion+Ioff))により計算します)を用いると、スピン偏極率Pは次のように書くことができます。
![]() (4.7)
(4.7)
ここで(4.6)式を見ると、波長の長いものに対しては周期の短いエコーシグナルが、波長の短いものについては周期の長いエコーシグナルが得られることが分かるでしょう。
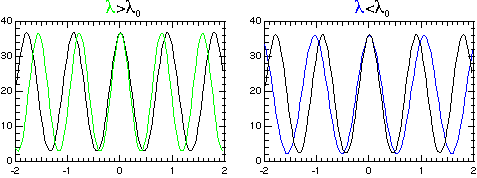 |
|
|
実際の入射中性子は単一の波長を含むわけではなく、ある波長分布を持っています。従って実際の測定データは、これら違う波長のエコーシグナルを重ね合わせた(畳み込んだ)ものとなります。
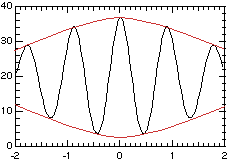 |
|
|
ここで赤で描いた振幅の減少プロファイルは波長分布スペクトルのフーリエ変換になっています。これは装置によって決まるだけでなく、厳密にはQの値や試料等のいろいろな条件によって違います。しかしその違いはデータ解析上は本質的ではないので、普通は次の経験的な関数形を用います。
![]() (4.8)
(4.8)
従って通常の実験では、あるQとtの値を決めて図4.5のようなプロファイルを測定し、式(4.8)を用いたフィッティングでAとBを求めます。更にflipping ratioの測定をします。この測定を試料と標準試料について行い、両者について得られたスピン偏極率P、P'より中間相関関数の値を求めることになるのです。