

| KEK | YITP | arXiv | INSPIRE | Yahoo | Nat.Geo. |

 "Trans-Planckian Physics and Inflation: An Introduction of Renormalizable and Background-Free Quantum Gravity"
By Ken-ji Hamada (Fundamental Theories of Physics 223, Springer Nature, 2025)
詳しくは、Springer Nature Link: Trans-Planckian Physics and Inflation、及び著書の項目を参照。
"Trans-Planckian Physics and Inflation: An Introduction of Renormalizable and Background-Free Quantum Gravity"
By Ken-ji Hamada (Fundamental Theories of Physics 223, Springer Nature, 2025)
詳しくは、Springer Nature Link: Trans-Planckian Physics and Inflation、及び著書の項目を参照。
量子重力理論の目的はPlanckスケールを超えた世界のダイナミクスを明らかにすることです。そこでは重力の量子的ゆらぎが大きく、距離の概念が失われたいわゆる背景時空独立な世界が実現していると考えられます。最近の研究から、そのようなスケールの無い世界が共形変換の下でのゲージ同値性、すなわちBRST共形不変性として表現できることが分かってきました。それは特定の背景時空上を運動する重力子の量子化ではなく、時空そのものの量子化を意味しています。ここで紹介するくり込み可能な重力の量子論はPlanckスケールを超えた高エネルギー世界をBRST共形不変性をもつ特別な共形場理論で記述し、さらにそこからの破れの程度を表す無次元の重力結合定数を持った理論です。以下、この理論のことを漸近的背景自由な量子重力理論(Asymptotically Background-Free Quantum Gravity)と呼ぶことにします。
詳しくは、著書及び解説書の項目を参照。
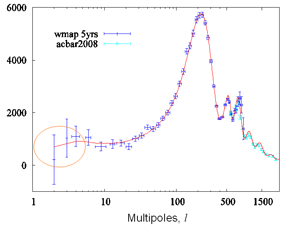
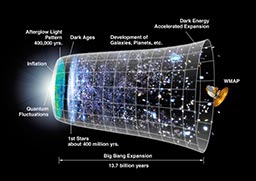
現在の宇宙は共形不変性が破れた世界です。この理論はその破れを表す新しい力学的スケールの存在も予言しています。その値をPlanckスケールより2桁低い10^17GeVとすると、宇宙が共形不変な量子時空からインフレーションの時代を経て、力学的スケールで量子相関が短距離になり、時空が相転移を起こして、古典的なFriedmann時空に移行する進化のシナリオを構成することができます。この理論の強みは、インフラトン場のような余分な自由度を導入することなく、重力場のダイナミクスだけでそれができることです。COBEやWMAP人工衛星が観測したCMBスペクトルの大角度成分には、時空が量子的だった当時のスペクトルの情報がそのまま保存されていると考えられます。左図の赤線は理論値で、○で囲まれた大角度成分の落ち込みは量子重力理論の力学的スケールの存在を示唆しています。また、インフレーション期間の長さ(e-foldings)とスカラー振幅の大きさはPlanckスケールと力学的スケールの比を用いて説明することができます。[量子重力的宇宙論の研究論文]
背景時空独立性は時間や空間の概念が喪失していることを表しています。一方、量子重力の力学的スケールが示す相関距離は、それよりも長距離では量子相関が切れて、その性質が無くなることを表しています。このことは、この相関距離が物理的に測定可能な最小の距離であることを示しています。このように時空は、離散化することなしに連続体のまま、この長さ単位で実質的に量子化されていることになります。また、量子重力の素励起(以下で説明)はこの力学的スケールを単位として現れると考えられます。
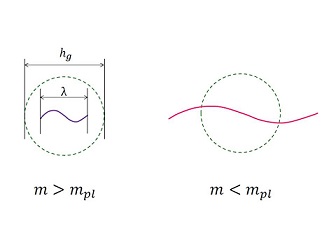
理論の詳細を記述する前に、Einstein重力理論の限界について、それを越えるために時空の相転移の考えが必要であることを簡単に説明しておきます。良く知られた問題点として特異点の存在や、繰り込み不可能性がありますが、もう少し異なる表現をしてみます。いま、質量mの素粒子があるとします。その量子的な大きさを表すCompton波長は1/mで与えられます。一方、この粒子のSchwarzschild半径はm/m_p^2で与えられます。ここで、m_pはPlanck質量スケールです。このことは、もしm > m_pならば粒子がホライズンの内側に隠れてしまって、その粒子の情報が消えてしまうことを意味します。これは強い重力場で起こるユニタリ性問題で、Planckスケールを越えた高エネルギー世界では粒子はブラックホールになり、通常の記述がもはや成り立たなくなることを示唆しています。そのため、場の量子論を考えるときは通常Planckスケールで紫外カットオフを導入しなければならなくなります。一般的に、背景時空に依存した理論ではこの紫外カットオフが必要になります。それは宇宙項問題の元凶にもなっています。
以下で説明する量子重力理論はそのような紫外カットオフが無い理論です。そして、理論が予言する時空の相転移は、最初にも述べたように、重力場が強くなると時空構造が変化して背景時空独立な世界が実現し、背景時空上を伝播する粒子的記述そのものが成り立たなくなることを意味します。これによって、上記の問題を根本的に解決することができます。
Einstein重力理論はくりこみ不可能な理論であることは良く知られています。それは、スカラー曲率で定義されるEinstein作用が量子論的に不安定な下に有界でない作用であることと関係しています。ただ、理論の基礎となるもっとも大切な一般座標変換不変性がくりこみ理論と矛盾しているわけではありません。ここで紹介する繰り込み可能な重力の量子論は下に有界な作用を用いて定義されます。それは、一般座標変換不変性とWess-Zumino積分可能条件の二つの条件から決まる以下の作用で与えられます [くり込みに関する研究論文]:

ここで、第一項は共形不変なWeyl作用です。その前の"t"が漸近自由性を示す無次元のくりこみ可能な結合定数で、重力場のトレースレステンソルモードのダイナミクスを支配します。第二項はEuler項で、その前の係数 b は t で展開されます。一方、時空全体のスケールを表す共形モードのダイナミクスを記述するために通常導入されるスカラー曲率の2乗の項は、積分可能条件を満たさないために排除されています。ここが以前の重力理論とは大きく異なるところです。この理論では、共形モードのダイナミクスは積分測度から誘導されるWess-Zumino作用 S によって記述され、分配関数は以下のように表されます:
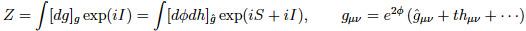
このとき、共形モードには新たな結合定数を導入していないことに注意してください。結合定数 t の最低次で現れるWess-Zumino作用は特にRiegert作用と呼ばれ、
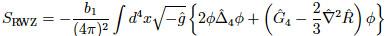
で与えられます。ここで重要な点は、共形モードを厳密に、非摂動的に量子化していることです。実際それが可能だということです。その結果、理論は非摂動的な場の量子論の代表格である共形場理論(Conformal Field Theory, CFT)を用いて表されます。共形不変性の存在によって特異点は排除され、ブラックホールにおける情報喪失パラドクスのようなユニタリ性の問題を議論することが可能になります。一方、結合定数は共形不変性からのズレの度合いを測るものさしの役目を果たしています。漸近自由性を示すその結合定数が低エネルギーで大きくなると古典的な時空に相転移します。このような紫外極限で背景時空独立性が現れる性質のことを通常の漸近自由性と区別して漸近的背景自由性(Asymptotic Background Freedom)と呼ぶことにします。[共形場理論と物理状態に関する研究論文]
昨今、量子重力理論と称するモデルが数多く報告されていますが、量子補正を具体的に計算することができるモデルは多くはありません。ここで紹介した量子重力理論はまさに計算できる理論です。計算可能な理論の一つであるストリング理論との違いは、まず定義されるている時空の次元が異なります。高エネルギー極限で共形不変性を持つかどうかも大きな違いです。また、ストリング理論は明白に有限な理論のため、有効作用は新たなスケールを含まない局所的なものになります。そのためストリング長さ以外の力学的スケールはコンパクト化を通して導入されます。これに対して、繰り込み可能な量子重力理論は繰り込み操作によって有効作用が非局所的になり、量子色力学(QCD)と同様に、上記の作用関数に含まれるスケール以外に新しい力学的スケールが現れます。この力学的スケールの重要性は上で述べた通りです。
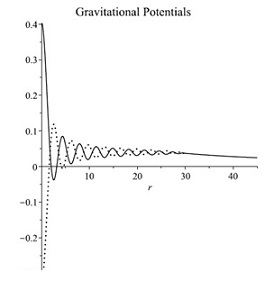
Planck質量より大きな質量をもつ点状の粒子は、Einsteinの重力理論ではブラックホールになってしまう。何故なら、そのような粒子の情報は自身のホライズンの内側に隠れて失われてしまうからである。これに対して、漸近的背景自由な量子重力では、Planck質量を超える質量を持った局所的な励起状態が存在する。その直径はおよそ相関距離で与えられ、Planck長さより2桁大きいサイズになる。右図はPlanck 質量の2倍の質量を持った励起状態の解で、実線と点線はそれぞれ重力ポテンシャルである。Planck長さは1と規格化している。外側 (r>30) はSchwarzschild解で表され、内側は重力の量子効果が発動して、時空が大きく揺らいだ特異点のない構造になっている。ホライズンも量子効果で消えて外部から見れば粒子に他ならないこの純粋に重力的な励起状態のことを暗黒粒子と呼ぶ。このように重力の量子効果を考えるとEinstein重力理論の問題を解決することが出来る。[K. Hamada, Phys. Rev. D102 (2020) 026024, arXiv:2005.06743]
量子重力インフレーション宇宙論では、宇宙はインフレーション時代におよそ10^30倍、Friedmann時空に移行してからさらに10^29倍、合わせておよそ10^59倍ほど膨張したと考えられます。それは、現在の銀河団よりも大きな数百メガパーセクのサイズがインフレーション以前ではPlanck長さ内に納まっていたことを意味します。左図は上記の量子重力理論の有効作用から重力場のゆらぎ(重力ポテンシャル)の発展方程式を導いて、インフレーション時空解のまわりで解いた結果です。Planck時間以前から時空の相転移(ビッグバン)が起こる時間までを数値計算していて、横軸は物理時間です。初めは大きかったゆらぎの振幅がインフレーション期間中に小さくなって、相転移時(図右端)では10^-5の観測値に近づくことが示されています。このように、量子重力インフレーションでは原始ゆらぎの小ささが、微調整ではなく、動力学的に説明することが出来ます。このゆらぎの情報が相転移の過程で乱されないのは、インフレーション期にその波長が大きく引き伸ばされて、量子重力の相関距離よりも十分に大きなスケールまで成長しているからです。それ故、インフレーション以前の宇宙創成期のスケール不変なスペクトルの情報がそのまま時空相転移後の熱的な宇宙に転写され、それがCMBのゆらぎスペクトルに中に受け継がれて今日それを観測することが出来るのです。[K. Hamada, S. Horata and T. Yukawa, Phys. Rev. D81 (2010) 083533, arXiv:0908.0192].
宇宙定数は一般座標不変性から決して否定されない。むしろ存在する方が自然である。実際、前世紀の終わりにRiessとSchmidtやPermutterらによって主導された実験によってそれは発見された。宇宙定数の問題とは、その存在が問題なのではなく、それに対するゼロ点エネルギーからの量子補正を計算すると観測値よりも120桁も大きな値になってしまうことである。その際、通常、Planckスケールに紫外カットオフを導入して計算が行われる。一方、一般座標不変性から導かれる全ハミルトニアンがゼロになるという拘束条件は、ゼロ点エネルギーが消えることを一般論として示している。この矛盾はどこから来るのか。それは紫外カットオフが一般座標不変性を壊す計算方法だからである。逆に言えば、一般座標不変な方法で計算すれば宇宙定数問題は生じないということである。このように問題の根本原因はPlanckスケールを超えた世界を正しく記述できていなかったことである。漸近的背景自由な量子重力理論は真にハミルトニアン拘束条件が背景自由性として厳密に成り立つ繰り込み可能な場の量子論で、宇宙定数問題は生じない。[K. Hamada, arXiv:2204.03914]

![]() "Trans-Planckian Physics and Inflation: An Introduction of Renormalizable and Background-Free Quantum Gravity"
By Ken-ji Hamada (Fundamental Theories of Physics vol. 223, Springer Nature, 2025)
"Trans-Planckian Physics and Inflation: An Introduction of Renormalizable and Background-Free Quantum Gravity"
By Ken-ji Hamada (Fundamental Theories of Physics vol. 223, Springer Nature, 2025)
| Preface | ||
| Contents | ||
| Chapter 1 | What Quantum Gravity Should Reveal | |
| Chapter 2 | Renormalizable and Background-Free Quantum Gravity | |
| Chapter 3 | Conformal Invariance as Background Freedom | |
| Chapter 4 | Physical Meaning of Hamiltonian/Momentum Constraints | |
| Chapter 5 | Renormalization Using Dimensional Regularization | |
| Chapter 6 | BRST Conformal Algebra and Physical States | |
| Chapter 7 | Quantum Gravity Inflation | |
| Chapter 8 | Localized Massive Excitations of Quantum Gravity | |
| Chapter 9 | What the Cosmological Constant Problem Is | |
| Chapter 10 | Amplitude Reduction of Spacetime Fluctuations and Primordial Spectra | |
| Chapter 11 | Topology and Quantum Gravity | |
| Chapter 12 | Simplicial Quantum Gravity | |
| Finale | ||
| Appendix | A, B, C, D | |
| References |

| 目次 | ||
| 第1章 | はじめに | |
| 第2章 | Minkowski共形場理論 | |
| 第3章 | Euclid共形場理論 | |
| 第4章 | 2次元共形場理論の基礎 | |
| 第5章 | 共形異常とWess-Zumino作用 | |
| 第6章 | 2次元量子重力理論 | |
| 第7章 | 4次元量子重力理論 | |
| 第8章 | 量子重力の物理状態 | |
| 第9章 | 重力相殺項と共形異常 | |
| 第10章 | くり込み可能な量子重力理論 | |
| 第11章 | Einstein理論の宇宙 | |
| 第12章 | 量子重力的宇宙論 | |
| 第13章 | 宇宙論的摂動論 | |
| 第14章 | 量子重力ゆらぎからCMB多重極まで | |
| 付録 |
量子重力理論の目的はPlanckスケールを超えた高エネルギー世界を明らかにすることである。そこでは重力の量子的ゆらぎが大きく、時間や距離の概念が失われたいわゆる背景時空独立な世界が実現すると考えられる。特定の時空を運動する粒子の描像はもはや無く、時空そのものの量子化が必要とされる。本書で紹介するくり込み可能な重力の量子論はそのような世界を共形場理論を用いて記述し、そこからのズレを摂動的に定式化した理論である。
はじめに共形場理論の一般的な事柄について解説した後、背景時空独立な量子重力理論が特別な共形場理論として記述できることを示す。共形不変性がゲージ対称性である一般座標不変性の一部として現れ、共形変換によって結びつく異なる背景時空上の理論がゲージ同値になることでその独立性が表現される。前半ではその変換を生成するBRST演算子を構成し、量子重力の物理的場の演算子や状態について解説する。
後半ではくり込み可能な量子重力理論を一般座標不変性が明白に保たれる次元正則化を用いて定式化する。その際、共形場理論からのズレを表す無次元の重力結合定数を導入する。そのベータ関数が負になることから、共形不変な世界が紫外領域で実現することが示される。一方で、その破れを表す力学的赤外スケールLambda_QGの存在も予言される。その値を10^17GeVとすると、スケール不変な原始宇宙がPlanckエネルギー付近から指数関数的に膨張を始め、Lambda_QG付近でその不変性が完全に壊れた現在の古典的な宇宙に相転移するインフレーションモデルを構成することが出来る。その発展の運動方程式の考察から相転移時のパワースペクトルを求め、CMBの観測結果と照合する。


| Contents | ||
| Section 1 | Introduction | |
| Section 2 | Renormalizable Quantum Gravity | |
| 2.1 Brief Summary of The Model | ||
| 2.2 Conformal Invariance and Physical States | ||
| 2.3 Renormalization | ||
| Section 3 | Numerical Quantum Gravity | |
| Section 4 | Cosmology | |
| Section 5 | Conclusion |
多くの人はPlanck長さよりも短距離の世界は存在しないと考えている。あるいは、その世界は一般座標不変性とは異なる物理法則によって支配されているのではないかと考えている。Planck長さにカットオフを入れ、それを量子化された時空の実体であると考えている事がその表れである。何故そう考えるのか。問題はどこにあるのか。重力の理論が抱えている、時空の特異点、繰り込み可能性、ユニタリ性、宇宙定数、原始ゆらぎの起源、時間とは、などに関する多くの問題は、結局のところ、Planckスケールの世界を場の量子論としてどのように記述するかという問題なのである。本稿の主題は、それらの問題を解き明かしながら、Planckスケールの壁の向こう側を記述するための一つの道を提示することである。
三次元以上の共形場理論の最近の発展についての解説書。Minkowski及びEuclid共形場理論の基礎、演算子積(OPE)、Conformal Blocks、ユニタリ性バウンドなど。また、これらについて解説したスライド D=3, 4共形場理論の最近の発展について も参照。
ゲージ不変な宇宙論的摂動論、Sachs-Wolfe関係式、CMB異方性スペクトルほか。何故Planckスケールの現象が現在のCMBの観測から分かるのかを理解するための解説書。
二次元量子重力理論
その他
INSPIREによる論文リスト