"Trans-Planckian Physics and Inflation: An Introduction of Renormalizable and Background-Free Quantum Gravity"
　　　　By Ken-ji Hamada (Fundamental Theories of Physics 223, Springer Nature, 2025)
　　　　For details, see Springer Nature Link: Trans-Planckian Physics and Inflation, or Books

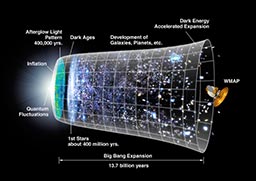
The discovery of the cosmic microwave background radiation (CMB) by Penzias and Wilson has proven that the universe was once a melting pot of high energy reactions at its early stage, and since then it has been cooling as it expands. Valuable information on physical processes taking place in the expanding universe has been recorded in the CMB as tiny anisotropies. Angular power spectra of the anisotropies, recently observed by the Cosmic Background Explorer (COBE) and the Wilkinson Microwave Anisotropy Probe (WMAP), are, roughly speaking, projection of the history for the period between its birth to the present. It gives us a amazing hope that if we believe the idea of inflationary universe describing a extremely rapid expansion without global thermalization, the long-distance correlation in observed anisotropies can provide the information about dynamics of the period before the universe grew to the Planck scale. We are now on the stage of revealing and verifying the quantum aspect of universe.

After passing many theoretical as well as experimental tests, the general theory of relativity has been established as the fundamental theory of gravity capable of describing the evolution of universe. Many questions in the mysteries of universe have arose expecting that the theory can give answers, such as, how the universe is created, why it is expanding, how it will evolve in the future, and so on. In order to answer these questions, we need to know the initial condition of the universe that would be set at the Planck time. However, it is the period when quantum mechanics rules the law of universe, and it is beyond the power of the classical general relativity. If we wish to apply the Einstein theory for the Planck scale phenomena, it has fatal difficulties, such as the black hole singularity and divergences in the canonical quantization procedure. Existence of these problems makes us wonder whether the Planck scale is the upper limit of the energy beyond which nature cannot be described in terms of physical laws. It is our ultimate task to construct the quantum theory which breaks the wall of Planck scale and creates a new frontier.

Renormalizable quantum theory of gravity developed on the basis of the conformal gravity in four dimensions provides an evolutional scenario of the universe which starts from quantum states with conformal invariance, passing through the inflationary era, and then makes transition to the conventional Einstein spacetime without adding any artificial field by hands. In this theory, the gravitational (metric tensor) field is written as a product of the conformal factor and the traceless tensor, and the conformal factor that primarily governs distance is treated strictly while the traceless tensor field is handled in perturbation. The renormalized coupling of the traceless tensor mode indicates the asymptotic freedom. It implies that at very high energies beyond the Planck mass scale, quantum fluctuations of the conformal factor are large and dominant; consequently the background freedom, or background independence in quantum spacetime, is realized and spacetime is nonsingular. This nature is called "asymptotic background freedom'' to distinguish from the normal asymptotic freedom. The power-law spectrum obtained from the two point correlation function of scalar curvature shows a significant character of the conformally invariant field theory which is expected to be observed cosmologically.

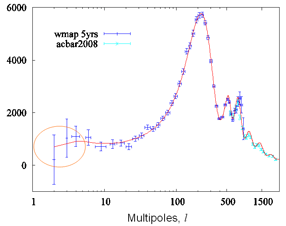
The asymptotic background freedom also implies that there exists a dynamical scale where the effective coupling of traceless tensor mode diverges, and the conformal symmetry loses its validity. About this point the universe is expected to make a transition from the quantum spacetime to the classical Einstein spacetime, and fluctuations of the conformal mode would be frozen to the classical background. Such a dynamical scale is given by the order of 10^17GeV below the Planck scale. The sharp fall off of the angular power spectra at low multipole components of anisotropies in the CMB is expected to be an appearance of dynamical scale. [Research papers on quantum gravity cosmology]

《Novel Interpretation of Minimal Length》

The inverse of the dynamical energy scale mentioned above gives the correlation length of quantum gravity. If shorter than this length, we cannot measure the distance, which is due to the background-metric independence where the concept of time and space is lost. Thus, it represents the minimal length of space-time we can measure physically. In this sense, space-time is practically quantized by this length unit without descretizing it. The energy of excitations in quantum gravity would be then given by the dynamical scale. If there is a stable excitation, it becomes a candidate for dark matter.

《Limitations of Einstein's Theory of Gravity and Spacetime Phase Transitions》

Before describing the details of the theory, let us briefly explain the limitations of Einstein's theory of gravity and why the concept of a spacetime phase transition is necessary to overcome them. While the existence of singularities and non-renormalizability are well-known issues, we can express the problem in a slightly different way. Suppose there is an elementary particle of mass m. Its Compton wavelength, which represents its quantum size, is given by 1/m. On the other hand, the Schwarzschild radius of this particle is given by m/m_p^2, where m_p is the Planck mass scale. This implies that if m > m_p, the particle becomes hidden inside its horizon, causing the information of that particle to be lost. This is a unitarity problem that arises in strong gravitational fields. It suggests that in a high-energy world beyond the Planck scale, particles become black holes, and conventional descriptions no longer hold. Therefore, when considering quantum field theory, a ultraviolet (UV) cutoff must typically be introduced at the Planck scale. Generally, theories that depend on a background spacetime require the UV cutoff, which is also the root cause of the cosmological constant problem.

《Ostrogradsky's Classic Theorem is Inapplicable to Quantum Gravity》

The classic theorem by Ostrogradsky in 1850 underpins the fact that all known mechanical systems, including Newtonian mechanics, are formulated using second-order or lower derivatives. In general terms, this theorem shows that higher-derivative mechanical systems become unphysical systems containing ghosts that make the Hamiltonian unbounded from below. The fact that Einstein's theory of gravity is defined by second-order derivatives is also not unrelated to the existence of this theorem. Nevertheless, it is important to note here that quantum gravity systems, where the total Hamiltonian is strictly constrained to zero, are inherently outside the scope of this old theorem. Rather, in gravitational systems, ghosts are an indispensable entity for constructing spacetime. In fact, the Friedmann universe and astronomical bodies formed by gravity cannot be constructed without the existence of ghost modes. This condition, generally referred to as the Hamiltonian and momentum constraints, can be expressed in renormalizable quantum gravity as an identity within the Schwinger-Dyson equations, such as

However, if we adopt the conventional weak-field (graviton) approximation approach, which reduces the gravitational system to a Lorentz-invariant system of special relativity, the condition that the total Hamiltonian vanishes is practically shelved, making this old theorem effective. This approach, which considers graviton scattering, is an approximation method applicable only in energy regimes sufficiently below the Planck scale, where the distortion of the background spacetime caused by the presence of gravitons is negligibly small, that is, the backreaction to the background spacetime can be ignored. To describe trans-Planckian physics, we need a quantization of gravity where the total Hamiltonian vanishes, fully incorporating the backreaction. This means quantizing spacetime itself, and doing so in a way that satisfies "background freedom," where the laws of physics do not depend on a specific background spacetime. The quantum gravity theory defined below satisfies this condition. [K. Hamada, arXiv:2608.17364]

《Asymptotically Background-Free Quantum Gravity》

It is well known that Einstein's theory of gravity is a non-renormalizable theory. This issue is closely related to the fact that the Einstein-Hilbert action, defined by the scalar curvature, is quantum-mechanically unstable and not bounded from below. However, the most fundamental and important principle of the theory, diffeomorphism invariance, does not inherently contradict renormalization theory. The quantum theory of gravity introduced here is defined using an action that is bounded from below. This specific action is uniquely determined by two key conditions of diffeomorphism invariance and renormalizability. It is given by the following expression [Research papers on renormalization in quantum gravity] :

The first term is the Weyl action and "t" is the dimensionless coupling constant with negative beta function, which controls dynamics of the traceless tensor field. On the other hand, the conformal factor in the gravitational field is treated non-perturbatively without introducing its own coupling constant. The path integral over the gravitational field is described as

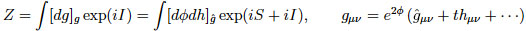
Here, S is the Wess-Zumino action for conformal anomalies induced from the path integral measure. It is a Jacobian required to preserve diffeomorphism invariance when rewriting the path integral using the practical measure defined on the background metric. Especially, the action S that appears at the ultraviolet (UV) fixed point of t=0 is called the Riegert-Wess-Zumino action, which is given by

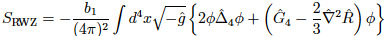
At the UV fixed point, the theory is described as a special conformal field theory (CFT). Exact conformal symmetry comes out as part of quantum diffeomorphism invariance, realized by taking the sum over all possible conformally flat configurations. The background freedom is then represented as a gauge equivalency under conformal transformations, called BRST conformal symmetry. This is nothing but a realization of the ``asymptotic safety" program proposed by S. Weinberg in 1970s, as a condition for quantum gravity to be well-defined. [Research papers on physical states and conformal field theory]

The BRST conformal field theory represents a strong coupling phase in which gravity is fully fluctuating. On the other hand, the coupling t, which measures a degree of devitation from the CFT, describes another strong couping phase. With the increase of it, spacetime will make a transition from quantum gravity phase to classical Einstein phase, as mentioned above.

《Localized Massive Excitation of Quantum Gravity》

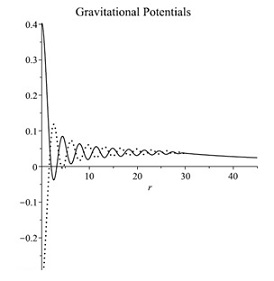
Point-like particles with mass greater than the Planck mass become black holes within Einstein's theory of gravity. This is because information of such particles is hidden inside their own horizon and lost. On the other hand, in the asymptotically background-free quantum gravity, there is a localized excited state with a mass exceeding the Planck mass. Its diameter is given by the correlation length, which is two orders of magnitude larger than the Planck length. The figure on the right shows a solution of the excited state with twice the Planck mass, in which the solid and dotted lines are two independent gravitational potentials. The Planck length is normalized to be 1 here. The outside (r> 30) is represented by the Schwarzschild solution, and the inside has a structure without singularities in which quantum effects of gravity are activated and spacetime fluctuates greatly. This purely gravitational excited state, in which the horizon disappears due to the quantum effect and is nothing but a particle when viewed from the outside, is called a dark particle. Considering the quantum effect of gravity in this way, the problem of Einstein's theory of gravity can be solved. [K. Hamada, Phys. Rev. D102 (2020) 026024, arXiv:2005.06743]

《Dynamical Description of Smallness of Primordial Fluctuations》

Quantum gravity inflation suggests that the universe expanded about 10^30 times during the inflationary era, and further 10^29 times after the transition to the Friedmann spacetime, about 10^59 times in total. That means that the size of hundreds of Megaparsecs, larger than the current cluster of galaxies, was within the Planck length before inflation. The figure on the left is the result of deriving evolution equations for gravitational fluctuations (gravitational potentials) from the effective action of the above quantum gravity theory and solving them around the inflation solution. Numerical calculation is performed from before the Planck time to the time when the spacetime phase transition (big bang) occurs, where the horizontal axis is physical time. It is shown that the amplitude of the fluctuations, which was initially large, becomes smaller during the inflation period and approaches the observed value of 10^-5 at the time of the phase transition (far right in the figure). In this way, quantum gravity inflation can explain the smallness of primordial fluctuations dynamically, not by fine-tuning. Information of this fluctuations is not disturbed in the process of the phase transition because its wavelength is greatly extended during the inflation period and grows to a scale sufficiently larger than the correlation length of quantum gravity. Therefore, information of scale-invariant spectra before inflation is transferred to the thermal universe after the spacetime phase transition as it is, and it is inherited in the CMB temperature fluctuation spectra and can be observed today. [K. Hamada, Universe 10 (2024) 33, arXiv:2306.01384]

《Solution to Cosmological Constant Problem and Background Freedom》

The cosmological constant is never denied from diffeomorphism invariance. Rather, it is more natural to exist. Indeed, it was discovered at the end of the last century by experiments led by Permutter, Riess and Schmidt. The problem with the cosmological constant is not its existence, but that the calculated quantum correction by zero-point energy is 120 orders of magnitude larger than the observed value. At that time, the calculation is usually performed by introducing an ultraviolet cutoff into the Planck scale. On the other hand, a constraint that the whole Hamiltonian derived from diffeomorphism invariance vanishes indicates that zero-point energy vanishes. Where does this contradiction come from? This is because the UV cutoff is a computational method that breaks the diffeomorphism invariance. Conversely speaking, the problem of the cosmological constant does not arise if it is calculated by a diffeomorphism invariant method. In this way, the root cause of the cosmological constant problem is that the world beyond the Planck scale had not been described correctly. The asymptotic background-free quantum gravity theory is truly a renormalizable quantum field theory in which the Hamiltonian constraint exactly holds as the background freedom, and the cosmological constant problem does not occur. [K. Hamada, PTEP 2022 (2022) 103E02, arXiv:2204.03914]

PROFILE

• Name: Ken-ji HAMADA
• Affiliation: Institute of Particle and Nuclear Studies, KEK, Tsukuba, Japan
• Research Interests: Renormalizable Quantum Gravity, Conformal Field Theory and Cosmology

RESEARCH ACTIVITIES

Books

"Trans-Planckian Physics and Inflation: An Introduction of Renormalizable and Background-Free Quantum Gravity"
　　　　By Ken-ji Hamada (Fundamental Theories of Physics vol. 223, Springer Nature, 2025)

	Preface
	Contents
	Chapter 1	What Quantum Gravity Should Reveal
	Chapter 2	Renormalizable and Background-Free Quantum Gravity
	Chapter 3	Conformal Invariance as Background Freedom
	Chapter 4	Physical Meaning of Hamiltonian/Momentum Constraints
	Chapter 5	Renormalization Using Dimensional Regularization
	Chapter 6	BRST Conformal Algebra and Physical States
	Chapter 7	Quantum Gravity Inflation
	Chapter 8	Localized Massive Excitations of Quantum Gravity
	Chapter 9	What the Cosmological Constant Problem Is
	Chapter 10	Amplitude Reduction of Spacetime Fluctuations and Primordial Spectra
	Chapter 11	Topology and Quantum Gravity
	Chapter 12	Simplicial Quantum Gravity
	Finale
	Appendix	A, B, C, D
	References


[Abstract] This book comprehensively describes recent developments in the research of renormalizable quantum gravity, focusing on its application to physics beyond the Planck scale, particularly in inflationary cosmology. It challenges the notion that the Planck scale is an impassable barrier, addressing issues such as singularity, renormalizability, unitarity, time, primordial fluctuations, and the cosmological constant. To describe the trans-Planckian world, it is necessary to break away from the view of graviton scattering and carry out the quantization of spacetime itself. Utilizing conformal field theory techniques to achieve background freedom, the book presents a renormalizable quantum theory of gravity that overcomes the Planck-scale wall.

Historically, discussions on renormalizability of gravity declined due to ghost issues. However, ghosts are essential in gravitational systems where the total Hamiltonian/momentum vanishes strictly, for aspects such as cosmic entropy, the formation of the universe, and gravitational objects. Quantum gravity approaches known in recent years often break diffeomorphism invariance or sacrifice renormalizability to eliminate ghosts. In contrast, this book presents a novel attempt which maintains that these are guiding principles even in the trans-Planckian domain, but constrains ghosts to be unphysical. The renormalizability implies a new scale that leads to a quantum gravity inflation scenario with a spacetime phase transition as the Big Bang. This book offers fresh insights into the trans-Planckian physics for graduate students and researchers.

"Quantum Gravity and Cosmology Based on Conformal Field Theory"
　　　　By Ken-ji Hamada (Cambridge Scholars Publishing, Newcastle, 2018) [

		Table of Contents
	Chapter 1	Introduction
	Chapter 2	Conformal Field Theory in Minkowski Space
	Chapter 3	Conformal Field Theory in Euclidean Space
	Chapter 4	Basis of Two-Dimensional Conformal Field Theory
	Chapter 5	Conformal Anomaly and Wess-Zumino Action
	Chapter 6	Two-Dimensional Quantum Gravity
	Chapter 7	Background-Free Quantum Gravity
	Chapter 8	Physical States of Quantum Gravity
	Chapter 9	Gravitational Counterterms and Conformal Anomalies
	Chapter 10	Renormalization in Quantum Gravity
	Chapter 11	The Universe in Einstein Gravity
	Chapter 12	Quantum Gravity Cosmology
	Chapter 13	Cosmological Perturbation Theory
	Chapter 14	From Quantum Gravity to CMB
	Appendix	A, B, C, D, E
	Bibliography


[Abstract] In this book, I will describe a renormalizable quantum gravity formulated with incorporating a new technique based on conformal field theory which recently has made prominent progress. Conformal invariance here appears as a gauge symmetry that gives a key property of quantum gravity known as the background-metric independence. Due to the presence of this symmetry, the theory becomes free from the problem of spacetime singularity, and thus from the information loss problem, namely the ghost problem as well. Furthermore, I will give a new scenario of the universe that evolves from quantum gravity world to the current classical world through the spacetime phase transition, including inflation driven by quantum gravity effects only.

This book also includes descriptions of recent developments in conformal field theory, renormalization theory in curved space, and conformal anomalies related thereto, almost of which do not found in other books. In addition, it includes review on evolution equations of the universe that is the foundation of modern cosmology necessary to understand results of the CMB experiments such as WMAP. Furthermore, it will be briefly shown that there is a noticeable relationship between the quantum gravity and a random lattice model that is based on the dynamical triangulation method known as another description of the background free property. I would like to describe these topics by taking enough pages as a latest advanced textbook for leading to this new area of quantum field theory that developed mainly since the beginning of this century.

		Contents
	Section 1	Introduction
	Section 2	Renormalizable Quantum Gravity
		2.1 Brief Summary of The Model
		2.2 Conformal Invariance and Physical States
		2.3 Renormalization
	Section 3	Numerical Quantum Gravity
	Section 4	Cosmology
	Section 5	Conclusion


[Abstract] Tracing the history of the universe, spacetime in its early epoch would be totally fluctuating quantum mechanically, and there would be no classical spacetime to describe dynamics. The models of quantum gravity we are going to discuss are aimed to describe such states with background-metric independence and transitions to the conventional spacetime dynamics.

The first model we choose is a renormalizable theory of gravity developed on the basis of the conformal gravity in four dimensions. In this theory the metric tensor field is written as a product of the conformal factor and the traceless tensor, and the conformal mode is treated non-perturbatively while the traceless tensor field is handled as a perturbation. The renormalized coupling of the traceless mode indicates the asymptotic freedom. It implies that at very high energies beyond the Planck mass scale, quantum fluctuations of the conformal field are dominated as a consequence of the background-metric independence. The second model we plan to discuss is a numerical method for quantizing gravity carried on the simplicial spacetime manifold. The theory treats dynamics non-perturbatively within the limited space allowed in a cluster of computers. It is significant that these two theories seem to be in the same universality class so far as the critical exponents are compared. It means that a conformal invariant spacetime can be mapped to a simplicial manifold with varying connectivity of simplices.

The asymptotic freedom also implies that there exists a dynamical scale where the effective coupling of traceless mode diverges, and the conformal symmetry loses its validity. About this point the universe is expected to make a transition from the quantum spacetime to the classical Einstein spacetime, and fluctuations of the conformal field would be frozen to the classical background. The primordial power spectrum obtained from the two point correlation function of scalar curvature shows a significant character of the theory which is expected to be observed cosmologically. The sharp fall off of the angular power spectra at low multipole components of anisotropies in the cosmic microwave background is a topic we wish to discuss.

Monograph

• "Into A World Beyond The Planck Scale That Nobody Knows" [PDF 156 pages]

  Many people believe that there is no world shorter than the Planck length, or that the world is governed by a physical law different from diffeomorphism invariance. Putting a cutoff in the Planck length and thinking of it as an entity of quantized sapcetime shows that. Why do you think so? What is the problem? Essential problems such as singularity, renormalizablity, unitarity, origin of primordial fluctuations, time, and so on ultimately come down to the problem of how to describe the trans-Planckian world as a continuum quantum field theory. The main purpose of this article is to solve these problems and present a way to describe the other side of the Planck scale wall.

Recent slides

• Quantum Gravity Effective Action Provides Entropy of The Universe
• Study of Nonlinear Evolution of Spacetime Fluctuations in Quantum Gravity Inflation
• Revealing A Trans-Planckian World Solves The Cosmological Constant Problem
• Massive Excited State of Quantum Gravity as a Dark Particle
• Asymptotically Background Free Quantum Gravity and Its Cosmological Implications
• BRST Conformal Symmetry and Quantum Gravity
• Gravitational Counterterms Near Four Dimensions and Conformal Anomalies
• Analyzing WMAP Observation by Quantum Gravity

Research papers (selected)

Quantum Gravity Cosmology

1. Quantum Gravity Effective Action Provides Entropy of The Universe,
   K. Hamada, Particles 7 (2024) 465, Special Issue Feature Papers for Particles 2023, arXiv:2401.09672[hep-th].
2. Study of Nonlinear Evolution of Spacetime Fluctuations in Quantum Gravity Inflation for Deriving Primordial Spectrum,
   K. Hamada, Universe 10 (2024) 33, arXiv:2306.01384[hep-th].
3. Revealing A Trans-Planckian World Solves The Cosmological Constant Problem,
   K. Hamada, PTEP 2022 (2022) 103E02, arXiv:2204.03914[hep-th].
4. Localized Massive Excitation of Quantum Gravity as a Dark Particle,
   K. Hamada, Phys. Rev. D102 (2020) 026024, arXiv:2005.06743[hep-th].
5. From CFT Spectra to CMB Multipoles in Quantum Gravity Cosmology,
   K. Hamada, S. Horata and T. Yukawa, Phys. Rev. D81 (2010) 083533, arXiv:0908.0192[astro-ph].
6. Space-time Evolution and CMB Anisotropies from Quantum Gravity,
   K. Hamada, S. Horata and T. Yukawa, Phys. Rev. D74 (2006) 123502, astro-ph/0607586.
7. CMB Anisotropies Reveal Quantized Gravity,
   K. Hamada and T. Yukawa, Mod. Phys. Lett. A20 (2005) 509, astro-ph/0401070.
8. Baryogenesis by Quantum Gravity,
   K. Hamada, A. Minamizaki and A. Sugamoto, Mod. Phys. Lett. A23 (2008) 237, arXiv:0708.2127 [astro-ph].

Renormalization in Quantum Gravity

1. Diffeomorphism Invariance Demands Conforml Anomalies,
   K. Hamada, Phys. Rev. D102 (2020) 125005, arXiv:2010.06771[hep-th].
2. Physical Cosmological Constant in Asymptotically Background Free Quantum Gravity,
   K. Hamada and M. Matsuda, Phys. Rev. D96 (2017) 026010, arXiv:1704.03962[hep-th].
3. Two-Loop Quantum Gravity Corrections to Cosmological Constant in Landau Gauge,
   K. Hamada and M. Matsuda, Phys. Rev. D93 (2016) 064051, arXiv:1511.09161[hep-th].
4. RG Analysis for Quantum Gravity with A Single Dimensionless Coupling,
   K. Hamada, Phys. Rev. D90 (2014) 084038, arXiv:1407.4532[hep-th].
5. Determination of Gravitational Counterterms Near Four Dimensions from RG Equations,
   K. Hamada, Phys. Rev. D89 (2014) 104063, arXiv:1403.4354[hep-th].
6. Resummation and Higher Order Renormalization in 4D Quantum Gravity,
   K. Hamada, Prog. Theor. Phys. 108 (2002) 399, hep-th/0203250.
7. Background-metric Independent Formulation of 4D Quantum Gravity,
   K. Hamada and F. Sugino, Nucl. Phys. B553 (1999) 283, hep-th/9810095.

Quantum Diffeomorphism, Physical States and Conformal Field Theory

1. Ostrogradsky's Theorem is Incompatible with Background Independence in Quantum Gravity,
   K. Hamada, arXiv:2608.17364[gr-qc].
2. BRST Conformal Symmetry as A Background-Free Nature of Quantum Gravity,
   K. Hamada, arXiv:1707.06351[hep-th][Review].
3. BRST Analysis of Physical Fields and States for 4D Quantum Gravity on R x S^3,
   K. Hamada, Phys. Rev. D86 (2012) 124006, arXiv:1202.4538[hep-th].
4. BRST Invariant Higher Derivative Operators in 4D Quantum Gravity based on CFT,
   K. Hamada, Phys. Rev. D85 (2012) 124036, arXiv:1203.4894[hep-th].
5. Background Free Quantum Gravity based on Conformal Gravity and Conformal Field Theory on M^4,
   K. Hamada, Phys. Rev. D85 (2012) 024028, arXiv:1109.6109[hep-th].
6. Conformal Field Theory on R x S^3 from Quantized Gravity,
   K. Hamada, Int. J. Mod. Phys. A24 (2009) 3073--3110, arXiv:0811.1647[hep-th].
7. Building Blocks of Physical States in a Non-Critical 3-Brane on R x S^3,
   K. Hamada, Int. J. Mod. Phys. A20 (2005) 5353--5398, hep-th/0402136.
8. Conformal Algebra and Physical States in a Non-critical 3-brane on R x S^3,
   K. Hamada and S. Horata, Prog. Theor. Phys. 110 (2003) 1169, hep-th/0307008.

Two Dimensional Quantum Gravity

1. Quantum Theory of Dilaton Gravity in 1 + 1 Dimensions,
   K. Hamada, Phys. Lett. B300 (1993) 322, hep-th/9206071.
2. Physical States, Factorization and Non-linear Structures in Two Dimensional Quantum Gravity,
   K. Hamada, Nucl. Phys. B413 (1994) 278, hep-th/9309094.
3. Ward Identities of W_infinity Symmetry in Liouville Theory coupled to c_M < 1 Matter,
   K. Hamada, Phys. Lett. B324 (1994) 141, hep-th/9311047.
4. Non-linear Structures in Non-critical NSR String,
   K. Hamada and H. Ishikawa, Commum. Math. Phys. 176 (1996) 401, hep-th/9405130.

Others