結晶からの散乱

F(k-k')=∫drρ(r) exp[i(k-k')・r]

のように表されます。ここで、 Q=k-k'とします。
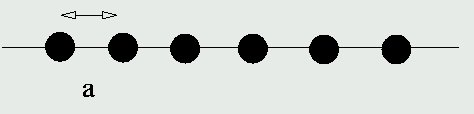
次に、長さaの周期がm回繰り返された構造で 実際に散乱振幅を計算してみます。

F(Q)=∫_0^ma drρ(r) exp[iQ・r] (積分範囲 0～ma)

F(Q)=Σ_n=0^m-1 exp(inqa) ∫_0^a drρ(r) exp[iQ・r]

F(Q)=(1-exp(imQa))/(1-exp(iQa))∫_0^a drρ(r) exp[iQ・r]

この式は、周期的に並んでいる構造で 散乱振幅を 計算するときは、長さaの周期の中の構造(単位胞)の積分計算をすれば、 後は (1-exp(imQa))/(1-exp(iQa))(Laue関数)の因子だけ 掛ければよいということを意味している。
通常の結晶では、mの値がアボガドロ数(6.02×10^23個)程度あり、 Laue関数は Qa=2πnのときのみ 値mを持つことになる。 (注: 位相の項を無視したとき) このとき Qa=2πnの条件は 何を意味しているだろうか？
Q=2ksinθ、k= 2π/λを 代入すると

2a sinθ=nλ

ピーンと来ましたか? そうです、ブラッグの法則 です。 このように、単に散乱振幅を積分で計算するだけで、ブラッグの法則は 導かれるのです。
つまり、結晶の場合は、ブラッグの法則が成り立つ点Q (逆格子点)でのみ 散乱振幅F(Q)が値を持つことになります。 以下の図に結晶からの散乱を X線写真で測定した実験結果を示します。
逆格子点でのみF(Q)が値を持ち 黒点として写真に写っています。

したがって、前節で 散乱振幅F(Q)を 測定すれば、物体の電子密度分布ρ(r)が求まるとしましたが、 結晶の場合、これらの逆格子点での散乱強度を収集すると、 単位胞内の電子密度分布ρ(r)が求まるわけです。

次に 長さaの周期が何回繰り返された構造なのかは どうすれば わかるでしょうか?
その情報は もちろん Laue関数がもっています。 mの値が あまりに大きい場合には、すでに上で述べたように Qa=2πnのときのみ 値を持ちます。 しかしながら、mの値が小さい場合には Qa=2πnのブラッグの法則を 満たさないQでも散乱振幅が値を持ちます。 以下の図は、m=4,m=6のときのf(x)=sin^2(mx)/sin^2(x)のグラフである。

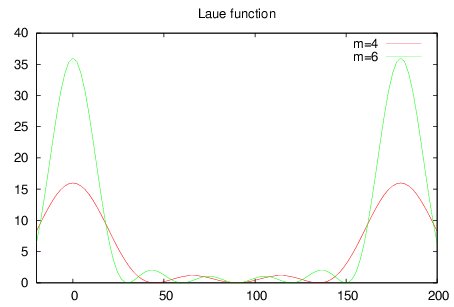
x=180°のときが Qa=2πに対応しており、ブラッグの法則が成立している。 さらに、Braggの法則が成り立たない領域に散乱強度が存在し、 かつ周期的な振動構造が観測される。 この周期的な振動構造より、mの値が決定できるのである。 例えば、m=4では 0、180°に観測されるブラッグ反射の間に 2つのピーク構造を示すことが m=4の特徴となっている。