Fourier変換（FT）

注釈

FTに先立ってBaseLine補正によりS(Q) = 1の周りに振動するように補正することを推奨

nvaSqの返り値（ELementContainer）を使ったFTの準備

最初にFourier変換のためのオブジェクトを作成する。 このオブジェクトの中には、S(Q)、Qなど必要なデータに加えて、Fourier変換による2体分布関数を得るための関数が格納されている。

In [3]: import nvaGr

In [4]: f90=nvaGr.FT(d90(0))
no of density atoms/angstrom^3:  0.06622
modification functoin:  0
説明：

  • nvaSqの返り値であるd90(0)を使ったFourier変換の準備。ここでは"f90"という名前のオブジェクトとして必要なデータを準備。（f90という名前は任意）

  • 数密度は、nvaSqの嵩密度を使わない設定になっている。デフォルトではシリカガラスの値になっている。

    • 数密度の指定方法　：　f90=nvaGr.FT(d90(0), 0.0333)　または　f90=nvaGr.FT(d90(0))実行後に、f90.set_rho(0.0333) またはf90.rho = 0.0333

  • 窓関数としてLorch関数を使用可能

    • f90.set_window(1)　または　f90.mod_number = 1

nvaGr.FT(infile[, rho = 0.06622])

Fourier変換のためのオブジェクトの生成

パラメータ

  • infile (name) -- データ名

  • rho (float) -- 試料数密度（省略するとシリカガラスの数密度が入る）

戻り値

Fourier変換のためのオブジェクト

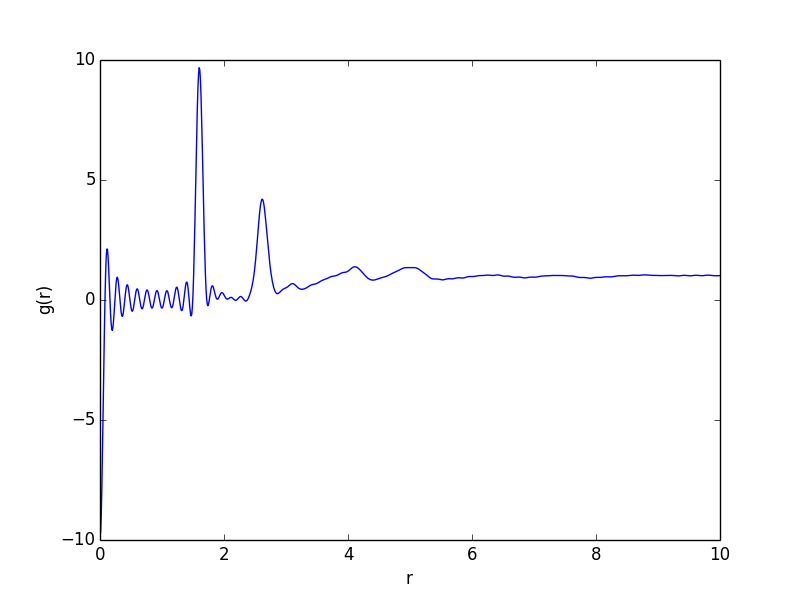
In [5]: f90.gr(10,0.01,0.9,40.0)
no of density  atoms/angstrom^3:  0.06622
rmax of g(r):  10
delta-r of g(r):  0.01
nonzero 0 4486
Q-range of S(Q) data 0.768293634837 to 68.5486184261
Qmin & Qmax for FT: 0.900736968724 40.0174019434
Q index min & max: 159 3950
説明

  • rmax = 10, \(\Delta\) r = 0.01, Qmin = 0.9, Qmax = 40でg(r)を計算

  • 指定したFourier変換のQ範囲は、入力S(Q)データのQ範囲を超える場合には、入力S(Q)データに合わせて自動調整。

nvaGr.gr(rmax, dr, qmin=0.0, qmax=65.0)

Fourier変換のためのオブジェクトの生成

パラメータ

  • rmax (float) -- 2体分布関数の最大r値（最大距離値）

  • dr (float) -- 2体分布関数のmath:Delta r　（距離bin幅）

  • qmin (float) -- Fourier変換に使用する最小Q値

  • qmax (float) -- Fourier変換に使用する最大Q値

戻り値

Fourier変換のためのオブジェクト内に格納される

g(r)のlow-rに生じるノイズの除去

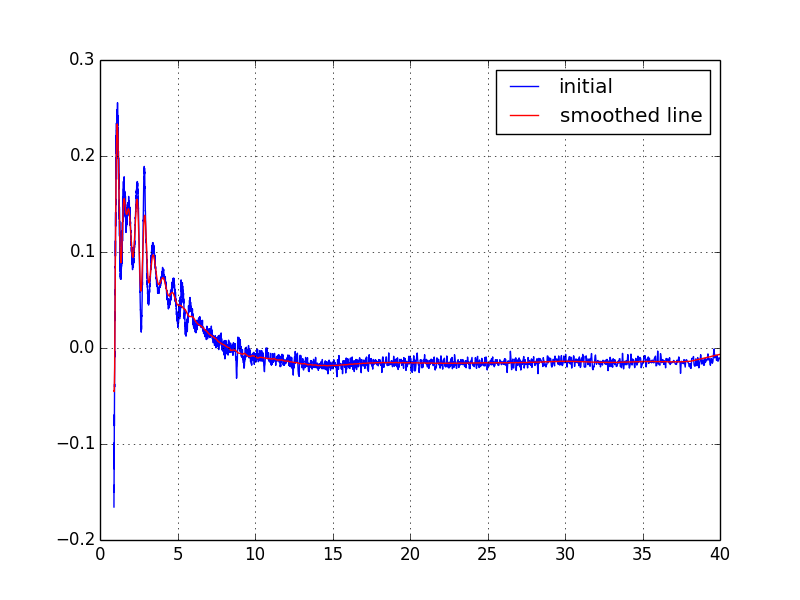
S(Q) = 1の周りに振動すべきS(Q)が、S(Q) = 1 から外れるなど正しく補正されていない場合に、g(r)のlow-rにノイズが生じる。 low-r領域で、試料中の最短原子間距離よりも小さなrに相関が現れる場合に、これをノイズと見なして除去する。 ただし、除去の前後で、high-r側にはほとんど影響が出ないこともあるので、完全に除去する必要がない場合もある。

In [6]: f90.RemoveRipplegr(1.25,100)
Make g(r) = 0.0 at r <= 1.25
Inverse Fourer Transforming
Smoothing of difference between original of inverese FT S(Q)

In [7]: f90.gr(10,0.01,0.9,40.0)
no of density  atoms/angstrom^3:  0.06622
rmax of g(r):  10
delta-r of g(r):  0.01
nonzero 0 3790
Q-range of S(Q) data 0.900736968724 to 39.9772791101
Qmin changed from 0.9  to  0.900736968724
Qmax changed from 40.0  to  39.9772791101
Qmin & Qmax for FT: 0.900736968724 39.9772791101
Q index min & max: 0 3790
説明：
  • RemoveRipplegrでは

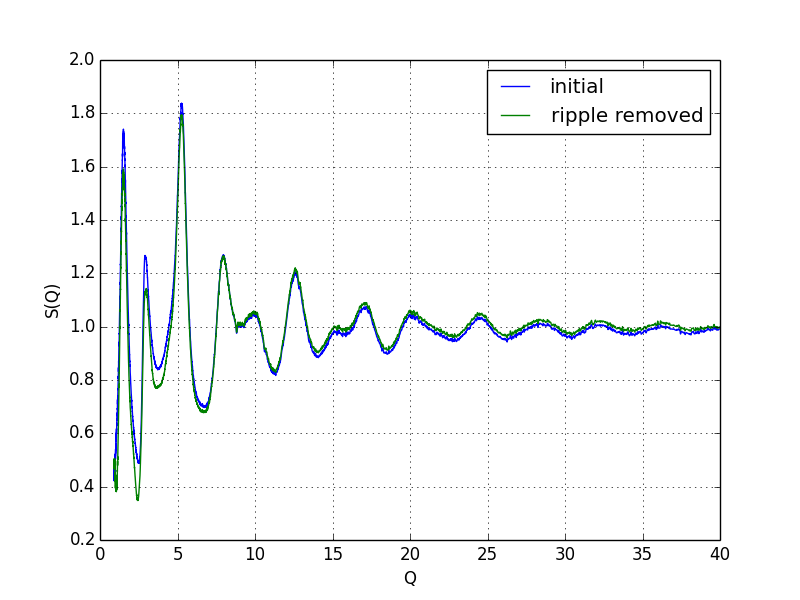
    • low-r (例ではr <= 1.25）でg(r) = 0として逆Fourier変換し、もとのS(Q)との差分をとることで、low-rノイズの原因となっている成分をS(Q)から除去する

    • 差分は移動平均で平滑化（例は100個の平均）

  • 差分を取り除いたS(Q)のデータは、自動的に格納されるので、再度Fourier変換可能

  • RemoveRipplegrとgrは何度でも繰り返し可能だが、Q範囲を広くしたい場合には最初からやり直し

../_images/FT_iFT.png ../_images/FT_difference.png ../_images/FT_2nd.png
(1)\[g(r) = 1 + \frac{1}{{2\pi^2 \rho r }}\int_{Q_{min}}^{Q_{max}} Q(S(Q)-1)\sin (Qr) {dQ}\]

さまざまな2体相関の計算

f90.gr(10,0.01,0.9,40.0) : g(r)
f90.Gr(10,0.01,0.9,40.0) : G(r), PDF
f90.RDF(10,0.01,0.9,40.0) : RDF
f90.Tr(10,0.01,0.9,40.0) : T(r)
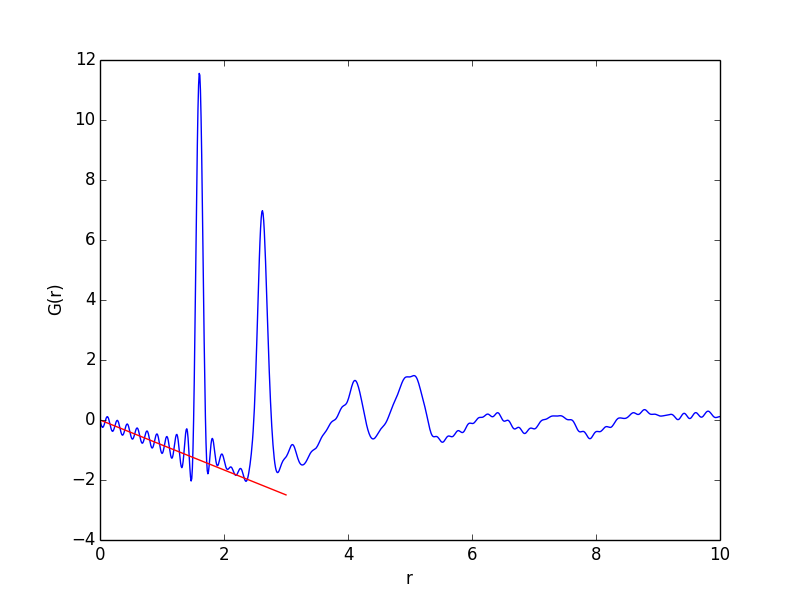
../_images/FT_Gr.png
(2)\[G(r) = 4\pi r \rho_{0} \left( g(r)-1 \right) = 4\pi r \left( \rho(r)-\rho_{0} \right) = \frac{2}{\pi}\int_{Q_{min}}^{Q_{max}} Q(S(Q)-1)\sin (Qr) {dQ}\]

それぞれのデータは、f90.gor, f90.Gr, f90.tor, f90.rdfに格納される。

4つの関数すべてを同時に計算することもできる。計算結果の格納先は、個別に計算する場合と同じ。

f90.CalcPDF(20.0,0.05,0.8,40.0)
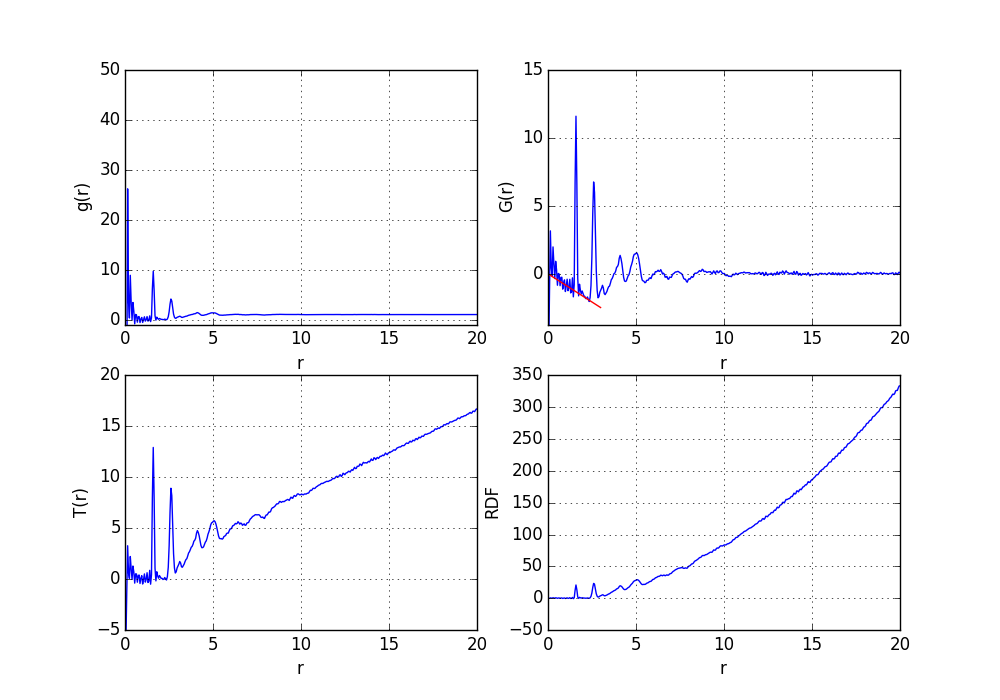
../_images/PDF_all.png

typeという変数により、一つの関数のみの画面出力を指定できる。

f90.CalcPDF(10.0,0.01,0.8,40.0,type="gr")
説明：

  • typeの指定: gr : g(r), Gr : G(r), tr : T(r), rdf : RDF

CalcPDFにより、4つの関数のデータが揃い、テキストデータ出力の準備が整う。CalcPDFの後で、RemoveRipplegrを実行し、CalcPDFを繰り返すことも可能。

Gauss関数のフィッティング

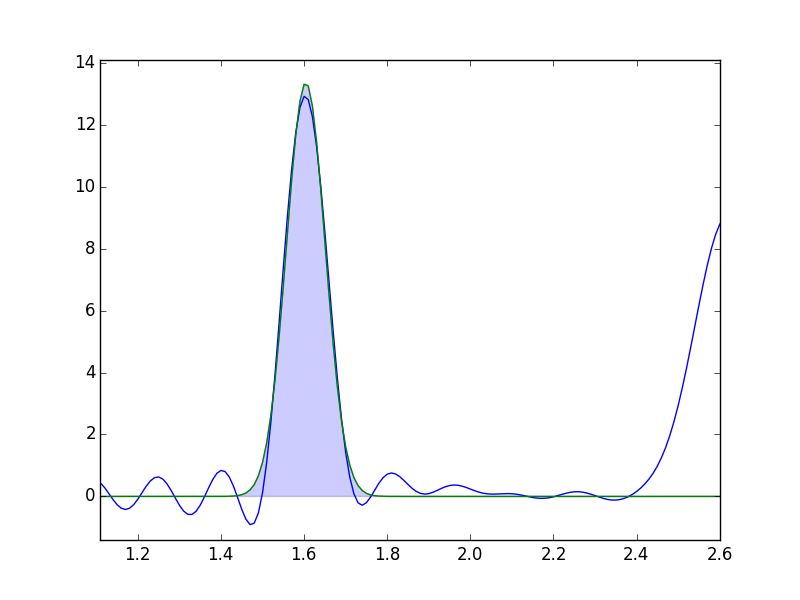
In [106]: nvaGr.gaussfit(f90.r, f90.tor, [12.0,1.6,0.1], 1.4, 1.8)
Gaussian fit results
 peak   : 13.3579801685
 center : 1.60412786477
 sigma  : 0.0465841908232
 area   : 0.116769249868
nvaGr.gaussfit(xdata, ydata, p0, rmin, rmax)

Gauss関数のfitting

パラメータ

  • xdata (list) -- x-axis data

  • ydata (list) -- y-axis data

  • p0 (list) -- [<gaussianのピーク値>,<gaussianの中心値>,<gaussianのsigma>]

  • rmin (float) -- fitするx軸の最小値

  • rmax (float) -- fitするx軸の最大値

戻り値

Gauss関数の面積

戻り値の型

float

../_images/gaussfit.png

テキストデータの出力

CalcPDFを行った後、g(r) G(r) T(r) RDFのテキストデータを出力する。

In [97]: f90.Output("test2.txt")
 --- Save g(r) G(r) T(r) RDF text data ---
      file name:  test2.txt

PDFguiのフォーマットでの出力

f90.OutPutForPDFgui(“pdfgui.txt”)

nvaSqのテキスト出力を読み込んで行うFT

In [45]: tt=nvaGr.FT("10708_sq_90_1steps.txt")
no of density atoms/angstrom^3:  0.06622
modification functoin:  0

In [46]: tt.gr(10,0.01,0.9,40.0)
no of density  atoms/angstrom^3:  0.06622
rmax of g(r):  10
delta-r of g(r):  0.01
nonzero 66 6851
Q-range of S(Q) data 0.76 to 68.61
Qmin & Qmax for FT: 0.9 40.0
Q index min & max: 80 3990