波の回折、干渉ついて

左側から平面波が入って来ます。
この平面波は、2箇所にスリットの切ってある板(図中に描かれていない)で、
遮られてます。すると、スリットの切られた部分で
回折が起き同心円状に広がる波ができます。
さらに2箇所から同心円状に広がる波同士が
干渉し、波と波が強め合っている部分と打ち消し合って波が
消失した部分ができます。
次にレーザー光を用いた実験をみてみよう。ここではスリットの代わりに
ガラス板に周期的な筋をつけた回折格子と呼ばれる物を使います。

上の計算で述べた 波の強め合っている部分と打ち消し合っている部分で
できた回折縞がハッキリとわかります。
この実験では、素性のわかった回折格子を用い、回折縞を観測していますが、
逆に回折縞を調べると どのような構造をもった回折格子なのかを
調べることも 出来ます。
また、測定する物体の大きさと、測定に用いる波の波長の大きさが
同程度であることが実験上たいへん重要となります。
上述のようなレーザーの実験では、波長0.0007mmで、
0.001~0.02mm程度の筋の間隔をもつ回折格子が使われます。
X線回折
すでに述べたように観測対象の大きさと同程度の
波の波長を用いた実験・測定が通常行われます。
また、下図(絵の所有権はPF
にあります)に示すように、
波長によって様々な種類の光があります。
したがって、測定したい物体の大きさに応じて、
ちょうど良い波長を持つ光が測定に利用されます。
例えば、数cmの構造を調べるためには、
波長 数cmのマイクロ波を用いることが出来ます。
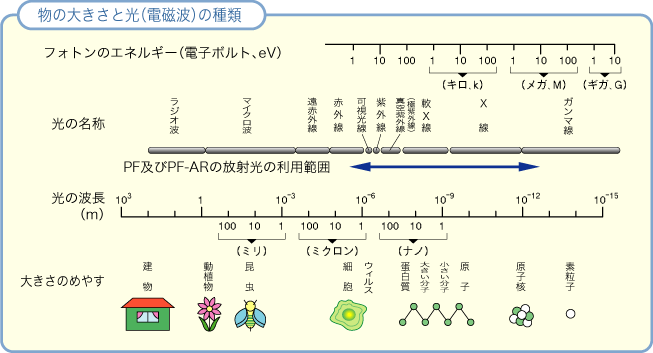
同様に、原子の配列構造である結晶構造を明らかにするために、
原子間距離に対応した波長を持つX線が利用されます。
このようなX線を用いた結晶からの回折のことを
X線回折(ブラック回折) と言います。
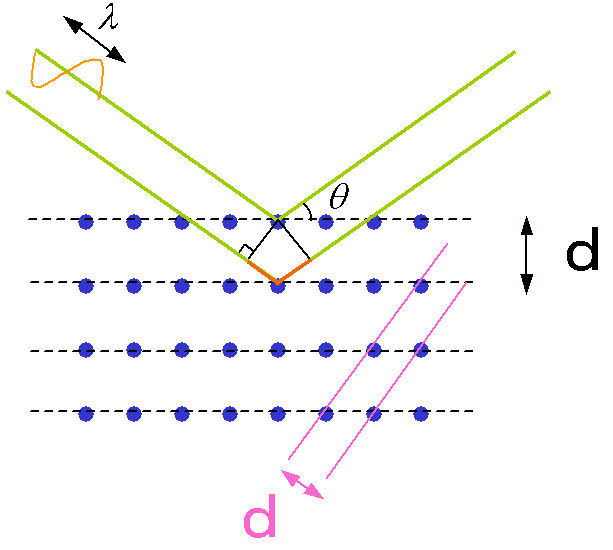
結晶内では、下図のように原子が周期的に配列しています。
ここで原子が整列した面を結晶面と言います。
点線やピンク線で示しているのが、この結晶面です。
この結晶で回折された波が強め合う条件を具体的に解いてみます。
面間隔dで並んだ結晶面に対し、X線がθの角度をもって入射し、
θの角度をもって出射する場合を考えます。
図のように 2つの面から散乱された波の行路差
(オレンジ線で示している部分)は、2dsinθです。
このとき X線の波長がλであれば、
波の位相差は2dsinθ/λであり、この位相差がちょうど
整数倍つまり2dsinθ/λ=nの時に、
2つの面で回折・散乱された光が強め合います。
これが、ブラッグの法則です。
したがって、このブラッグ法則によれば、
波が強め合う角度θが測定できれば、結晶内の面間隔dを決定することが
出来るわけです。
次>:
物体からの散乱



