断面積
基本
Fixed target experiment を想定する。
ビームが、ターゲットのある面積Aに均一に当たっているものとする。
(均一とみなせない場合は、均一とみなせるだけ小さな微小面積を考え、
後で積分すればよい。)
このうち、反応を起こした粒子の割合を、面積の比で表したものが断面積である。
標的一つ一つにある面積の的があって、そこにあたった場合だけ散乱し、そうでなければ素通りすると考えるとわかりよい。
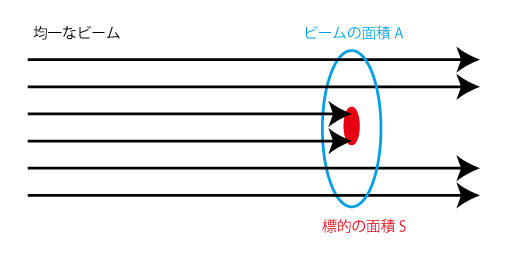
ターゲット粒子一つの的の大きさ、つまり断面積を$\sigma$とする。
ビームの当たっている面積Aの中に、ターゲット粒子は $n_b d \cdot A$個
存在しているので、ターゲット面積を全部あわせたもの、$S$は、
$$
S = \sigma \cdot n_b d \cdot A
$$
になる。つまり反応率$\dot{N}$は、
$$
\dot{N} = \frac{ \dot{N}_a }{A} \sigma n_b d \cdot A
$$
$$
\dot{N} = \dot{N}_a \sigma n_b d
$$
ワイヤーターゲット
ターゲットがワイヤー形状で、ビームがの径よりも太いとする。
