4.2) Guinier approximation

In order to investigate the behavior of I(Q) at very low angle, one can substitute the Mclaurin series,

, (4.13)

into eq. (4.9) gives

, (4.14)

where

, (4.15)

and

, (4.16)

in the vicinity of Q = 0 with restricting to the first two terms in eq. (4.13). The right-hand side of eq. (4.13) can be regarded as the first two terms of the Mclaurin series of function. Thus, to an accuracy of terms proportional to Q⁴, one can write for the beginning of the scattering curve

. (4.17)

This is the Guinier equation, derived about 60 years ago (Guinier, 1939). In order to relate parameters I(0) and R_G to the structure of a particle, one substitutes eq. (4.13) to the Debye equation (4.2) and obtain

. (4.18)

Comparing eq. (4.18) with eq. (4.14), one can deduce from the leading terms on the right-hand side that

, (4.19)

which is just the square of the total particle scattering length. From the comparison of the coefficients of the Q² terms, the following relation can be obtained,

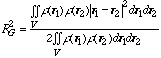, (4.20)

If one places the origin of coordinates at a point r₀, then simple calculations give

. (4.21)

It should be noted that the integrals in eq. (4.20) is independent of the actual position of the origin of coordinates, because both integrals are taken over the whole space. Hence one can match point r₀ with the center of mass of a particle. The second term in eq. (4.21) becomes zero and,

, (4.22)

which means that the radius of gyration of a particle about its center of mass.

Therefore, we have come to an important conclusion. In the very small-angle region, regardless of the structure of a particle, the scattering curve can be described with only two parameters: I(0), characterizing the total amount of scattering objects, and R_G, bearing information on its distribution with respect to the particle center of mass. For example, the radius of gyration of a uniform spherical particle with radius R can be simply calculated as

. (4.23)

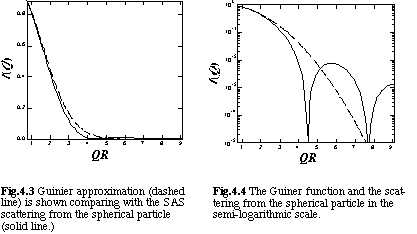
In Figs. 4.3 and 4.4, the Guinier function is plotted as a function of QR with the accurate solution for the spherical particle with radius R, which is the same curve shown in Figs. 4.1 and 4.2. From these figures, one can notice that the Guinier approximation is applicable only at the region of QR < p.

By taking a natural logarithm of equation (4.17), one has

, (4.24)

therefore, R_G can be determined from the slope of the linear part of the ln I(Q) - Q² plot, which is called the "Guinier plot". The same data shown in Fig. 4.3 are indicated in Fig. 4.5. Expressions for the radius of gyration via the dimensions of simple uniform geometrical bodies are summarized in Table 4.1.

The accuracy of calculation of R_G depends on a number of factors. (Details should be referred to another textbook; for example, Section 3.3 in Feigin and Svergun, 1987.) Therefore, one has to be careful to estimate the Guinier radius from observed scattering curves.

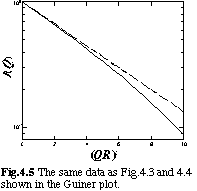
Sphere of Radius R
Spherical shell with radii R1 > R2
Ellipse with semiaxes a and b
Ellipsoid with semiaxes a, b, c
Prism with edges A, B, C
Elliptical cylinder with semiaxes a and b and height h
Hollow circular cylinder with radii R1 > R2 and height h
Table 4.1 Radii of gyration of some homogeneous bodies.